
【题目】到空间不共面的四点距离相等的平面的个数为( )
A.1个
B.4个
C.7个
D.8个
【答案】C
【解析】解:当空间四点不共面时,则四点构成一个三棱锥,如图:①当平面一侧有一点,另一侧有三点时,令截面与四棱锥的四个面之一平行,第四个顶点到这个截面的距离与其相对的面到此截面的距离相等,这样的平面有四个,②当平面一侧有两点,另一侧有两点时,即过相对棱的异面直线共垂线段的中点,且和两条相对棱平行的平面,满足条件.因三棱锥的相对棱有三对,则此时满足条件的平面个数是三个, 所以满足条件的平面共有7个,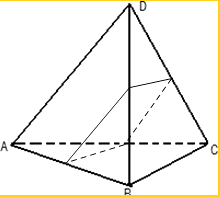
故选:C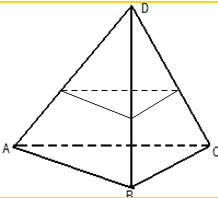
【考点精析】解答此题的关键在于理解平面的基本性质及推论的相关知识,掌握如果一条直线上的两点在一个平面内,那么这条直线在此平面内;过不在一条直线上的三点,有且只有一个平面;如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,D,E分别是BC,A1B1的中点. 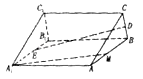
(1)求证:DE∥平面ACC1A1;
(2)设M为AB上一点,且AM= ![]() AB,若直三棱柱ABC﹣A1B1C1的所有棱长均相等,求直线DE与直线A1M所成角的正切值.
AB,若直三棱柱ABC﹣A1B1C1的所有棱长均相等,求直线DE与直线A1M所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣3x﹣10<0},B={x|m+1≤x≤2m﹣1}.
(1)当m=3时,求集合(UA)∩B;
(2)若A∩B=B,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A′B′C′中,AA′=2AC=2BC,E为AA′的中点,C′E⊥BE. 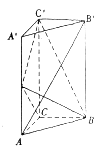
(1)求证:C′E⊥平面BCE;
(2)若AC=2,求三棱锥B′﹣ECB的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={a|一次函数y=(4a﹣1)x+b在R上是增函数},集合B= ![]() .
.
(1)求集合A,B;
(2)设集合 ![]() ,求函数f(x)=x﹣
,求函数f(x)=x﹣ ![]() 在A∩C上的值域.
在A∩C上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足(x﹣a)(x﹣3a)<0,其中a>0,命题q:实数x满足 ![]() .
.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1 , 则下列四个命题:
①P在直线BC1上运动时,三棱锥A﹣D1PC的体积不变;
②P在直线BC1上运动时,直线AP与平面ACD1所成角的大小不变;
③P在直线BC1上运动时,二面角P﹣AD1﹣C的大小不变;
④M是平面A1B1C1D1上到点D和C1距离相等的点,则M点的轨迹是过D1点的直线
其中真命题的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为贯彻落实教育部6部门《关于加快发展青少年校园足球的实施意见》,全面提高我市中学生的体质健康水平,培养拼搏意识和团队精神,普及足球知识和技能,市教体局决定举行春季校园足球联赛.为迎接此次联赛,甲中学选拔了20名学生组成集训队,现统计了这20名学生的身高,记录入如表:(设ξ为随机变量)
身高(cm) | 168 | 174 | 175 | 176 | 178 | 182 | 185 | 188 |
人数 | 1 | 2 | 4 | 3 | 5 | 1 | 3 | 1 |

(1)请计算这20名学生的身高的中位数、众数,并补充完成下面的茎叶图;
(2)身高为185cm和188cm的四名学生分别记为A,B,C,D,现从这四名学生选2名担任正副门将,请利用列举法列出所有可能情况,并求学生A入选门将的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com