
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为等腰梯形,
为等腰梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为线段
分别为线段![]() ,
, ![]() 的中点.
的中点.
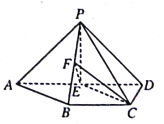
(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,
, ![]() ,求四面体
,求四面体![]() 的体积.
的体积.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)由线面平行的判定定理证明得到;(2)以![]() 为底面,点F到
为底面,点F到![]() 的距离为高,由于F为PB 的中点,所以点
的距离为高,由于F为PB 的中点,所以点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离的一半,算出体积。
的距离的一半,算出体积。
试题解析:(1)证明:连接![]() 、
、![]() ,
, ![]() 交
交![]() 于点
于点![]() ,
,
∵![]() 为线段
为线段![]() 的中点,
的中点, ![]() ,
, ![]() ,∴
,∴![]()
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() 为
为![]() 的中点,又
的中点,又![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)解法一:由(1)知,四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
∵四边形![]() 为等腰梯形,
为等腰梯形, ![]() ,
, ![]() ,
,
∴![]() ,∴三角形
,∴三角形![]() 是等边三角形,∴
是等边三角形,∴![]() ,
,
做![]() 于
于![]() ,则
,则![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,
,
又平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,∴点
,∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
又∵![]() 为线段
为线段![]() 的中点,∴点
的中点,∴点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离的一半,即
的距离的一半,即![]() ,又
,又![]() ,
,
∴![]()
![]() .
.
解法二: ![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,
的距离,
做![]() 于点
于点![]() ,由
,由![]() ,知三角形
,知三角形![]() 是等边三角形,∴
是等边三角形,∴![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,
,
又平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,∴点
,∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
又![]() 为线段
为线段![]() 的中点,∴
的中点,∴![]()
![]() ,
,
∴![]()
![]() .
.


科目:高中数学 来源: 题型:
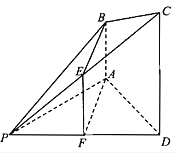
【题目】四棱锥![]() 中,已知
中,已知![]() 平面PAD,
平面PAD,![]() ,
,![]() ,E为棱PC上的一点,经过A,B,E三点的平面与棱PD相交于点F.
,E为棱PC上的一点,经过A,B,E三点的平面与棱PD相交于点F.
![]() 求证:
求证:![]() 平面PAD;
平面PAD;
![]() 求证:
求证:![]() ;
;
![]() 若平面
若平面![]() 平面PCD,求证:
平面PCD,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如图数阵的表格形式,表格内是按某种规律排列成的有限个正整数.

(1)记第一行的自左至右构成数列![]() ,
,![]() 是
是![]() 的前
的前![]() 项和,试求
项和,试求![]() 的表达式;
的表达式;
(2)记![]() 为第
为第![]() 行与第
行与第![]() 列交点的数字,观察数阵,若
列交点的数字,观察数阵,若![]() ,试求出
,试求出![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x∈R|x2-ax+b=0},B={x∈R|x2+cx+15=0},A∩B={3},A∪B={3,5}.
(1)求实数a,b,c的值;
(2)设集合P={x∈R|ax2+bx+c≤7},求集合P∩Z.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆的中心在原点,焦点在![]() 轴上,长轴长是短轴长的2倍且经过点
轴上,长轴长是短轴长的2倍且经过点![]() ,平行于
,平行于![]() 的直线
的直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,直线
,直线![]() 交椭圆于
交椭圆于![]() 两个不同点.
两个不同点.
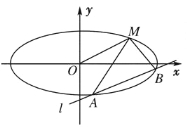
(1)求椭圆的方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 在抛物线
在抛物线![]() :
: ![]() 上,直线
上,直线![]() :
: ![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点,且直线
两点,且直线![]() ,
, ![]() 的斜率之和为-1.
的斜率之和为-1.
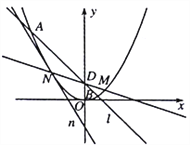
(1)求![]() 和
和![]() 的值;
的值;
(2)若![]() ,设直线
,设直线![]() 与
与![]() 轴交于
轴交于![]() 点,延长
点,延长![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,抛物线
,抛物线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,记直线
,记直线![]() ,
, ![]() 与
与![]() 轴围成的三角形面积为
轴围成的三角形面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 为双曲线
为双曲线![]() 的左、右焦点,过
的左、右焦点,过![]() 作垂直于
作垂直于![]() 轴的直线,在
轴的直线,在![]() 轴上方交双曲线
轴上方交双曲线![]() 于点
于点![]() ,且
,且![]() .
.

(1)求双曲线![]() 的两条渐近线的夹角
的两条渐近线的夹角![]() ;
;
(2)过点![]() 的直线
的直线![]() 和双曲线
和双曲线![]() 的右支交于
的右支交于![]() 、
、![]() 两点,求
两点,求![]() 的面积的最小值;
的面积的最小值;
(3)过双曲线![]() 上任意一点
上任意一点![]() 分别作该双曲线两条渐近线的平行线,它们分别交两条渐近线于
分别作该双曲线两条渐近线的平行线,它们分别交两条渐近线于![]() 、
、![]() 两点,求平行四边形
两点,求平行四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为利于分层教学,某学校根据学生的情况分成了A,B,C三类,经过一段时间的学习后在三类学生中分别随机抽取了1个学生的5次考试成缎,其统计表如下:
A类
第x次 | 1 | 2 | 3 | 4 | 4 |
分数y(满足150) | 145 | 83 | 95 | 72 | 110 |
![]() ,
, ;
;
B类
第x次 | 1 | 2 | 3 | 4 | 4 |
分数y(满足150) | 85 | 93 | 90 | 76 | 101 |
![]() ,
, ;
;
C类
第x次 | 1 | 2 | 3 | 4 | 4 |
分数y(满足150) | 85 | 92 | 101 | 100 | 112 |
![]() ,
, ;
;
(1)经计算己知A,B的相关系数分别为![]() ,
,![]() .,请计算出C学生的
.,请计算出C学生的![]() 的相关系数,并通过数据的分析回答抽到的哪类学生学习成绩最稳定;(结果保留两位有效数字,
的相关系数,并通过数据的分析回答抽到的哪类学生学习成绩最稳定;(结果保留两位有效数字,![]() 越大认为成绩越稳定)
越大认为成绩越稳定)
(2)利用(1)中成绩最稳定的学生的样本数据,已知线性回归直线方程为![]() ,利用线性回归直线方程预测该生第十次的成绩.
,利用线性回归直线方程预测该生第十次的成绩.
附相关系数 ,线性回归直线方程
,线性回归直线方程![]() ,
, ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com