


科目:高中数学 来源:不详 题型:填空题
| 志 愿 | 学 校 | 专 业 | |
| 第一志愿 | 1 | 第1专业 | 第2专业 |
| 第二志愿 | 2 | 第1专业 | 第2专业 |
| 第三志愿 | 3 | 第1专业 | 第2专业 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 钟K个人,当开放一个窗口时,40分钟后恰好不会出现排队现象;若同时开放两个窗口时,则15分钟分恰好不会出现排队现象。根据以下信息,若医院承诺5分钟后不出现排队现象,则至少需要同时开放的窗口数为 .
钟K个人,当开放一个窗口时,40分钟后恰好不会出现排队现象;若同时开放两个窗口时,则15分钟分恰好不会出现排队现象。根据以下信息,若医院承诺5分钟后不出现排队现象,则至少需要同时开放的窗口数为 .查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
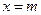 ,
,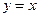 将圆面
将圆面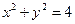 分成若干块,现有
分成若干块,现有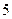 种颜色给这若干块涂色,每块只涂一种颜色,且任意两块不同色,共有
种颜色给这若干块涂色,每块只涂一种颜色,且任意两块不同色,共有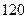 种涂法,则
种涂法,则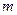 的取值范围是( )
的取值范围是( ) 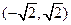 B.
B.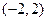
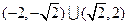 D.
D.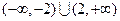
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com