
【题目】如图,直角![]() 中,∠
中,∠![]() ,
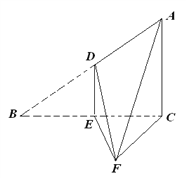
,![]() ,D、E分别是AB、BC边的中点,沿DE将
,D、E分别是AB、BC边的中点,沿DE将![]() 折起至
折起至![]() ,且∠
,且∠![]() .
.
(Ⅰ)求四棱锥F-ADEC的体积;
(Ⅱ)求证:平面ADF⊥平面ACF.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(Ⅰ)可作![]() 于
于![]() ,利用所给条件,可证
,利用所给条件,可证![]() 为棱锥底面上的高且求出其长度,再进一步求出底面梯形的面积,可求得四棱锥体积;(Ⅱ)取线段AF、CF的点N、Q,进一步证明
为棱锥底面上的高且求出其长度,再进一步求出底面梯形的面积,可求得四棱锥体积;(Ⅱ)取线段AF、CF的点N、Q,进一步证明![]() ,可证得两平面垂直.
,可证得两平面垂直.
试题解析:(Ⅰ)D、E分别是AB、BC边的中点,![]() 平行且等于
平行且等于![]() 的一半,
的一半,![]() ,
,![]()
依题意,![]() ,
,![]() ,∵
,∵![]() ,
,![]() ,∵
,∵![]() ,
,![]()
作![]() 于
于![]() ,则
,则![]() ,∵∠
,∵∠![]() ,
,![]()
梯形![]() 的面积
的面积![]()
四棱锥F-ADEC的体积![]()
(Ⅱ)(法一)取线段AF、CF的点N、Q,连接DN、NQ、EQ,则NQ平行且等于![]() 的一半,
的一半,![]() NQ平行且等于DE,DEQN是平行四边形,DN//EQ
NQ平行且等于DE,DEQN是平行四边形,DN//EQ
∵EC=EF,∠![]() ,
,![]() 是等边三角形,EQ
是等边三角形,EQ![]() ,又∵
,又∵![]() ,
,![]() ,
,![]() AC
AC![]() ,∵
,∵![]() ,
,![]()
![]() ,又
,又![]() ,
,![]()
(法二)连接BF,∵EC=EF,∠![]() ,
,![]() 是边长为2等边三角形
是边长为2等边三角形
∵BE=EF,![]() ,
,![]() ,
,![]()
![]() ,DE//AC,
,DE//AC,![]()
∵![]() ,
,![]() ,又∵
,又∵![]() ,,
,,![]()
又∵![]() ,
,![]()


科目:高中数学 来源: 题型:
【题目】把一颗骰子投掷两次,记第一次出现的点数为a,第二次出现的点数为b.已知方程组 ![]() .
.
(1)求方程组只有一个解的概率;
(2)若方程组每个解对应平面直角坐标系中点P(x,y),求点P落在第四象限的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x+1)ln x-a(x-1).
(1)当a=4时,求曲线y=f(x)在(1,f(1))处的切线方程;
(2)若当x∈(1,+∞)时,f(x)>0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
规定若满意度不低于98分,测评价该教师为“优秀”.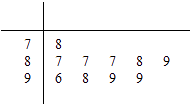
(1)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
记ξ表示抽到评价该教师为“优秀”的人数,求ξ的分布列及数学期望.
(2)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:x2=2py(p>0),直线y=kx+2与E交于A、B两点,且 ![]()
![]() =2,其中O为原点.
=2,其中O为原点.
(1)求抛物线E的方程;
(2)点C坐标为(0,﹣2),记直线CA、CB的斜率分别为k1 , k2 , 证明:k12+k22﹣2k2为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的极坐标方程为ρ=2cosθ,直线l的参数方程为 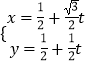 (t为参数),点A的极坐标为(
(t为参数),点A的极坐标为( ![]() ,
, ![]() ),设直线l与圆C交于点P、Q.
),设直线l与圆C交于点P、Q.
(1)写出圆C的直角坐标方程;
(2)求|AP||AQ|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,PC⊥平面ABC,PC=3,∠ACB= ![]() .D,E分别为线段AB,BC上的点,且CD=DE=
.D,E分别为线段AB,BC上的点,且CD=DE= ![]() ,CE=2EB=2
,CE=2EB=2 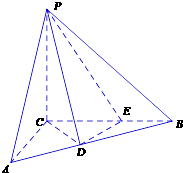
(1)证明:DE⊥平面PCD
(2)求二面角B﹣PD﹣C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com