
设α、β(α < β)是x的方程2x2-ax-2 = 0的两个实根,又![]() .
.
(Ⅰ)证明f ( α ) f ( β ) =-4;
(Ⅱ)判断函数f ( x )在[ α,β ]上的单调性,并予以证明;
(Ⅲ)当a取何值时,函数f ( x )在[ α,β ]上的最大值减去最小值的差最小,并说明理由.
解:(Ⅰ)由题设, ∴
(Ⅱ)任取x1,x2,使α ≤ x1 < x2≤β,则
其中 x2-x1 > 0, 又 4+a (x2 + x1)-4 x1x2 = -4α β + 2 (α + β) (x2 + x1)-4 x1x2 = -2α β-2α β + 2αx2+2αx1 + 2βx2 + 2βx1-2 x1x2-2 x1x2 = 2(x2 -β)( α-x1) + 2(x1 -β)( α-x2) > 0 . ∴ f ( x2 )-f ( x1 ) > 0,即f ( x2 ) > f ( x1 ) . ∴ f ( x )在[ a,b ]上是增函数. (Ⅲ) 由(Ⅱ),在[ α,β ]上f ( x )的最大值为f ( β ),最小值为f ( α ),又f ( α ) f ( β )=-4 < 0,故f ( β ) > 0,f ( α ) < 0 . ∴ f ( β )-f ( α ) = f (
β ) + [-f ( α )] 当且仅当f ( β ) = -f ( α ) = 2时,上式取等号. ∴ f ( β ) = 2时,f ( β )-f ( α )最小. 再由 ∴ a = 0时,f ( x )在[ α,β ]上最大值减最小值的差最小.
|
由题意得
|


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:
设A={x||x-1|<2},B={x|![]() >0},则A∩B等于
>0},则A∩B等于
A.{x|-1<x<3} B.{x|x<0或x>2}
C.{x|-1<x<0} D.{x|-1<x<0或2<x<3}
本题考查含绝对值不等式、分式不等式的解法及集合的运算.在进行集合运算时,把解集标在数轴上,借助图形可直观求解.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高一10月月考数学试卷(解析版) 题型:选择题
设集合M={x|0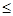 x<2},
x<2}, ,则有M∩N=( )
,则有M∩N=( )
A.{x|0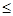 x<1} B.{x|0
x<1} B.{x|0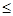 x<2}
x<2}
C.{x|0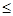 x
x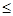 1} D.{x|0
1} D.{x|0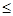 x
x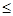 2}
2}
查看答案和解析>>
科目:高中数学 来源:2014届四川省高二4月数学试卷(解析版) 题型:解答题
设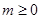 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量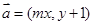 ,向量
,向量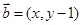 ,
,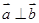 ,动点
,动点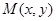 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程,并说明该方程所表示曲线的形状;
(2)已知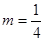 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且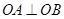 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;
(3)已知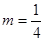 ,设直线
,设直线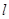 与圆C:
与圆C: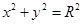 (1<R<2)相切于A1,且
(1<R<2)相切于A1,且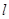 与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com