

 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
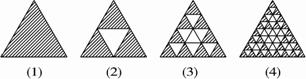
图中的三角形称为希尔宾斯基三角形,在下图4个三角形中,着色三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式,并在直角坐标系中画出它的图象.
 |  | ||||||||||||||
|
| ||||||||||||||
 |  | ||||||||||||||
| |||||||||||||||
| |||||||||||||||
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2008-2009学年北京市东城区高二模块测试数学试卷A(必修5)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com