
 ”的充分不必要条件( )
”的充分不必要条件( ) ”是否成立;再验证“
”是否成立;再验证“ ”⇒“M>N”是否成立,然后结合充要条件的定义即可得到答案.
”⇒“M>N”是否成立,然后结合充要条件的定义即可得到答案. 在R上单调递减,
在R上单调递减, ,
, ”的既不充分也不必要条件,故③错,
”的既不充分也不必要条件,故③错,

科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 2 |
| 3 |
| A、0 | B、1 | C、2 | D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| 1 |
| 4 |
| π |
| 16 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年陕西省高三第七次模拟考试理科数学试卷(解析版) 题型:填空题
下列结论中正确命题的序号是 .(写出所有正确命题的序号)
①积分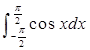 的值为2;
的值为2;
②若 ,则
,则 与
与 的夹角为钝角;
的夹角为钝角;
③若 ,则不等式
,则不等式 成立的概率是
成立的概率是 ;
;
④函数 的最小值为2.
的最小值为2.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省济南市高三一模数学文卷 题型:选择题
下列结论中正确命题的个数是
①命题p:“ ”的否定形式为
”的否定形式为 “
“ ;
;
② 若 是q的必要条件,则p是
是q的必要条件,则p是 的充分条件;
的充分条件;
③ “M>N”是“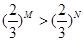 ”的充分不必要条件.
”的充分不必要条件.
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com