
设U=R,集合A={x|x2+3x+2=0},B={x|x2+(m+1)x+m=0},若( A)∩B=?,求m的值.
A)∩B=?,求m的值.
m=1或2
【解析】方法一:A={-2,-1},
由( A)∩B=?得B⊆A,
A)∩B=?得B⊆A,
∵方程x2+(m+1)x+m=0的判别式:
Δ=(m+1)2-4m=(m-1)2≥0,∴B≠?,
∴B={-1}或B={-2}或B={-1,-2}.
①若B={-1},则m=1;
②若B={-2},则应有-(m+1)=(-2)+(-2)=-4且m=(-2)·(-2)=4,这两式不能同时成立,
∴B≠{-2};
③若B={-1,-2},则应有-(m+1)=(-1)+(-2)=-3且m=(-1)·(-2)=2,由这两式得m=2.
经检验知m=1和m=2符合条件.∴m=1或2.
方法二:本题集合B中的方程的根是x1=-1,x2=-m.
当-m≠-1时集合B={-1,-m},此时只能A=B,即m=2;当-m=-1时集合B={-1},此时集合B是集合A的真子集,也符合要求.∴m=1或2.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(五)第二章第二节练习卷(解析版) 题型:选择题
已知函数f(x)=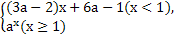 单调递减,那么实数a的取值范围是( )
单调递减,那么实数a的取值范围是( )
(A)(0,1) (B)(0, )
)
(C)[ ,
, ) (D)[
) (D)[ ,1)
,1)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(七)第二章第四节练习卷(解析版) 题型:选择题
已知函数f(x)=2x-2,则函数y=|f(x)|的图象可能是( )
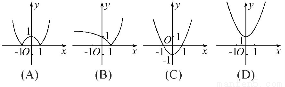
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(一)第一章第一节练习卷(解析版) 题型:选择题
已知集合A={x|x2+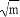 x+1=0},若A∩R=?,则实数m的取值范围是( )
x+1=0},若A∩R=?,则实数m的取值范围是( )
(A)m<4 (B)m>4
(C)0≤m<4 (D)0≤m≤4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业(一)第一章第一节练习卷(解析版) 题型:选择题
集合M={a,b},N={a+1,3},a,b为实数,若M∩N={2},则M∪N=( )
(A){0,1,2} (B){0,1,3}
(C){0,2,3} (D){1,2,3}
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十四第七章第三节练习卷(解析版) 题型:选择题
已知命题:①若点P不在平面α内,A,B,C三点都在平面α内,则P,A,B,C四点不在同一平面内;②两两相交的三条直线在同一平面内;③两组对边分别相等的四边形是平行四边形.其中正确命题的个数是( )
(A)0 (B)1 (C)2 (D)3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十五第七章第四节练习卷(解析版) 题型:选择题
设α,β是两个不同的平面,m,n是平面α内的两条不同直线,l1,l2是平面β内的两条相交直线,则α∥β的一个充分不必要条件是( )
(A)m∥β且l1∥α (B)m∥β且n∥l2
(C)m∥β且n∥β (D)m∥l1且n∥l2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com