
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
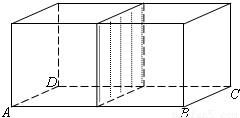
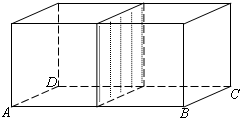 为了保护环境,南充市环保部门准备在工业园区拟建一座底面积为200平方米的长方体无盖二级净水处理池(如图所示),池深10米,池的外壁建造单价为每平方米400元,中间一条隔墙建造单价为每平方米100元,池底建造每平方米60元,试问:一般情况下,净水处理池的长AB设计为多少米时,可使总造价y最低?并求出此最值.
为了保护环境,南充市环保部门准备在工业园区拟建一座底面积为200平方米的长方体无盖二级净水处理池(如图所示),池深10米,池的外壁建造单价为每平方米400元,中间一条隔墙建造单价为每平方米100元,池底建造每平方米60元,试问:一般情况下,净水处理池的长AB设计为多少米时,可使总造价y最低?并求出此最值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
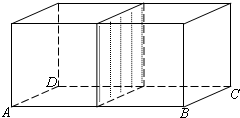
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com