

| A�� | �٢ڢ� | B�� | �ڢۢ� | C�� | �ڢܢ� | D�� | �ۢܢ� |
���� ��������ƽ�е��ж��������Ƿ���Եõ�����ƽ�У�ת��Ϊ����ƽ�У��õ�����ƽ�У�
��� �⣺��Ŀ�٣��۵�״̬�£���ͼ1�����������ȳ����ʱ����������治һ��ƽ�У�
��Ŀ�ڣ������У���ͼ2������OM=ON=O'M'=O'N'�����Եõ�����ƽ�У��Ӷ��õ�����ƽ�У�
��Ŀ�ۣ������У���ͼ2�������OK=OL=O'K'=O'L'�����Եõ�����ƽ�У��Ӷ��õ�����ƽ�У�
��Ŀ�ܣ�����ͼ3��������1=��2=��3=��4=90�㣬���Եõ�����ƽ�У��Ӷ��õ�����ƽ��
��Ŀ�ݣ�����ͼ3�������AB=A'B'=C'D'=CD����������治һ��ƽ�У�
��ѡ��B��
���� ���⿼��������ƽ��⇒����ƽ��⇒����ƽ�е�ת����ϵ�������е���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
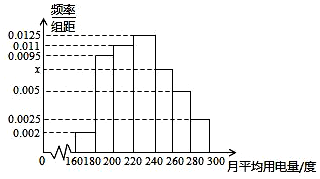 ij����100���������ƽ���õ�������λ���ȣ�����[160��180����[180��200����[200��220����[220��240����[240��260����[260��280����[280��300]�����Ƶ�ʷֲ�ֱ��ͼ��ͼʾ��
ij����100���������ƽ���õ�������λ���ȣ�����[160��180����[180��200����[200��220����[220��240����[240��260����[260��280����[280��300]�����Ƶ�ʷֲ�ֱ��ͼ��ͼʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {-1��0��1} | B�� | {-1��0} | C�� | {-2��-1��0} | D�� | {0��1��2} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | b��a��c | C�� | c��a��b | D�� | b��c��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
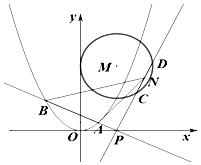 ��ͼ��������E��x2=2py��p��0���Ľ���Ϊ��0��1����Բ��M������y=2x��x��0�����Ұ뾶Ϊ2��ԲM��y�����У�
��ͼ��������E��x2=2py��p��0���Ľ���Ϊ��0��1����Բ��M������y=2x��x��0�����Ұ뾶Ϊ2��ԲM��y�����У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com