
 ,B产品的利润y2与投资金额x的函数关系为y2=
,B产品的利润y2与投资金额x的函数关系为y2= (注:利润与投资金额单位:万元).
(注:利润与投资金额单位:万元). ;(2) 分别用20万元和80万元资金投资A、B两种金融产品,可以使公司获得最大利润,最大利润为28万元.
;(2) 分别用20万元和80万元资金投资A、B两种金融产品,可以使公司获得最大利润,最大利润为28万元.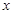 万元资金投入
万元资金投入 产品,利润
产品,利润 万元;
万元; 万元资金投入
万元资金投入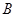 产品,利润
产品,利润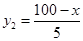 ,由
,由 可得所求函数关系;
可得所求函数关系;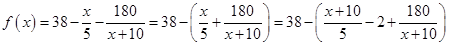
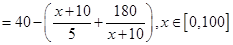 可考虑用基本不等式法求其最大值,并注意等号成立的条件。
可考虑用基本不等式法求其最大值,并注意等号成立的条件。 +
+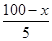
 -
- (x∈[0,100]). 6分
(x∈[0,100]). 6分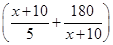 ,x∈[0,100],
,x∈[0,100],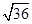 =28,取等号当且仅当
=28,取等号当且仅当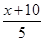 =
= 时,即x=20. 12分
时,即x=20. 12分

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源:不详 题型:解答题
 内单调递减,求a的取值范围;
内单调递减,求a的取值范围;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 是奇函数,(其中
是奇函数,(其中 )
)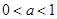 时,讨论函数f(x)的增减性;
时,讨论函数f(x)的增减性; 时,f(x)的值域是(1,
时,f(x)的值域是(1, ),求n与a的值。
),求n与a的值。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. | B.[-1,0] | C.(-∞,-2] | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com