
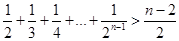
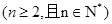 .
. 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源:不详 题型:单选题
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.人们通过大量试验得出抛硬币出现正面的概率为 |
| B.科学家通过研究老鹰的眼睛发明了电子鹰眼 |
| C.通过检验溶液的值得出溶液的酸碱性 |
| D.数学中由周期函数的定义判断某函数是否为周期函数 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 条直线, 这
条直线, 这 条直线任意两条不平行, 任意三条不共点, 记这
条直线任意两条不平行, 任意三条不共点, 记这 条直线将平面分成
条直线将平面分成 部分, 则
部分, 则 ___________,
___________, 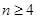 时,
时, _________________.)(用
_________________.)(用 表示).
表示).查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
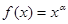 是增函数,而
是增函数,而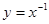 是幂函数,所以
是幂函数,所以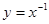 是增函数,上面推理错误是( )
是增函数,上面推理错误是( )| A.大前提错误导致结论错 | B.小前提错误导致结论错 |
| C.推理的方式错误导致错 | D.大前提与小前提都错误导致错 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com