
【题目】设椭圆中心在坐标原点,![]() 是它的两个顶点,直线
是它的两个顶点,直线![]() 与AB相交于点D,与椭圆相交于E、F两点.
与AB相交于点D,与椭圆相交于E、F两点.
(Ⅰ)若![]() ,求
,求![]() 的值;
的值;
(Ⅱ)求四边形![]() 面积的最大值.
面积的最大值.
【答案】(Ⅰ)解:依题设得椭圆的方程为![]() ,
,
直线![]() 的方程分别为
的方程分别为![]() ,
,![]() .············ 2分
.············ 2分
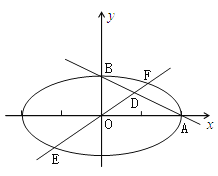
如图,设![]() ,其中
,其中![]() ,
,

且![]() 满足方程
满足方程![]() ,故
,故![]() .①
.①
由![]() 知
知![]() ,得
,得![]() ;
;
由![]() 在
在![]() 上知
上知![]() ,得
,得![]() .所以
.所以![]() ,
,
化简得![]() ,解得
,解得![]() 或
或![]() .················ 6分
.················ 6分
(Ⅱ)根据点到直线的距离公式和①式知,点![]() 到
到![]() 的距离分别为
的距离分别为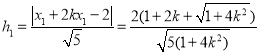 ,
,
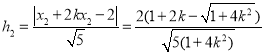 .9分
.9分
又![]() ,所以四边形
,所以四边形![]() 的面积为
的面积为
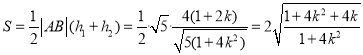
![]() ,
,
当![]() ,即当
,即当![]() 时,上式取等号.所以
时,上式取等号.所以![]() 的最大值为
的最大值为![]() .
.
【解析】
试题(Ⅰ)由题意易得椭圆方程,直线![]() 的方程,再设
的方程,再设![]() ,
,![]() 满足方程
满足方程![]() ,把
,把![]() 用坐标表示出来得
用坐标表示出来得![]() ,又点
,又点![]() 在直线
在直线![]() 上,则
上,则![]() ,根据以上关系式可解得
,根据以上关系式可解得![]() 的值;(Ⅱ)先求点E、F到AB的距离,再求
的值;(Ⅱ)先求点E、F到AB的距离,再求![]() ,则可得面积
,则可得面积![]() ,然后利用不等式求面积的最大值.
,然后利用不等式求面积的最大值.
试题解析:(I)依题意,得椭圆的方程为![]() , 1分
, 1分
直线![]() 的方程分别为
的方程分别为![]() , 2分
, 2分
如图设![]() ,其中
,其中![]() ,
,
![]() 满足方程
满足方程![]() 且故
且故![]() ,
,
由![]() 知
知![]() ,得
,得![]() , 4分
, 4分
由点![]() 在直线
在直线![]() 上知,
上知,![]() 得
得![]() , 5分
, 5分
![]() ,化简得
,化简得![]() 解得
解得![]() 或
或![]() . 7分
. 7分
(II)根据点到直线的距离公式和①式知,点E、F到AB的距离分别为
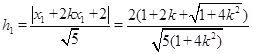 , 8分
, 8分
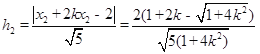 , 9分
, 9分
又![]() ,所以四边形AEBF的面积为
,所以四边形AEBF的面积为
![]()
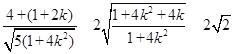 , 11分
, 11分
当![]() 即当
即当![]() 时,上式取等号,所以S的最大值为
时,上式取等号,所以S的最大值为![]() 13分
13分


科目:高中数学 来源: 题型:
【题目】对于任意的复数![]() ,定义运算
,定义运算![]() 为
为![]() .
.
(1)设集合![]() {
{![]() 均为整数},用列举法写出集合
均为整数},用列举法写出集合![]() ;
;
(2)若![]() ,
,![]() 为纯虚数,求
为纯虚数,求![]() 的最小值;
的最小值;
(3)问:直线![]() 上是否存在横坐标、纵坐标都为整数的点,使该点
上是否存在横坐标、纵坐标都为整数的点,使该点![]() 对应的复数
对应的复数![]() 经运算
经运算![]() 后,
后,![]() 对应的点也在直线
对应的点也在直线![]() 上?若存在,求出所有的点;若不存在,请说明理由.
上?若存在,求出所有的点;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1,3,5,7,9中任取3个数宇,与0,2,4组成没有重复数字的六位数,其中偶数共有( )
A.312个B.1560个C.2160个D.3120个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中志愿者部有男志愿者6人,女志愿者4人,这些人要参加元旦联欢会的服务工作. 从这些人中随机抽取4人负责舞台服务工作,另外6人负责会场服务工作.
(Ⅰ)设![]() 为事件:“负责会场服务工作的志愿者中包含女志愿者
为事件:“负责会场服务工作的志愿者中包含女志愿者![]() 但不包含男志愿者
但不包含男志愿者![]() ”,求事件
”,求事件![]() 发生的概率.
发生的概率.
(Ⅱ)设![]() 表示参加舞台服务工作的女志愿者人数,求随机变量
表示参加舞台服务工作的女志愿者人数,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于给定数列![]() ,如果存在实常数
,如果存在实常数![]() 使得
使得![]() 对于任意
对于任意![]() 都成立,我们称数列
都成立,我们称数列![]() 是“M类数列”.
是“M类数列”.
(1)若![]() ,数列
,数列![]() 是否为“M类数列”?若是,指出它对应的实常数
是否为“M类数列”?若是,指出它对应的实常数![]() ;若不是,请说明理由;
;若不是,请说明理由;
(2)证明:若数列![]() 是“M类数列”,则数列
是“M类数列”,则数列![]() 也是“M类数列”.
也是“M类数列”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com