
若实数a、b、c成等差数列,点P(–1, 0)在动直线l:ax+by+c=0上的射影为M,点N(0, 3),则线段MN长度的最小值是 .
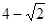
解析试题分析:因为a,b,c成等差数列,所以2b=a+c,即a-2b+c=0,可得方程ax+by+c=0恒过Q(1,-2),
又点P(-1,0)在动直线ax+by+c=0上的射影为M,所以∠PMQ=90°,
所以M在以PQ为直径的圆上,
所以此圆的圆心A坐标为(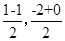 ),即A(0,-1),半径r=
),即A(0,-1),半径r= 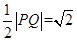 ,
,
又N(0,3),所以|AN|=  ,线段MN长度的最小值是
,线段MN长度的最小值是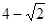 。
。
考点:等差数列的性质;直线关于点、直线对称的直线方程。
点评:此题考查了等差数列的性质,恒过定点的直线方程,圆周角定理,线段中点坐标公式,以及两点间的距离公式,利用等差数列的性质得到2b=a+c,即a-2b+c=0是解本题的突破点.


 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com