
已知椭圆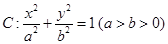 经过点
经过点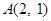 ,离心率为
,离心率为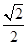 ,过点
,过点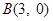 的直线
的直线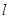 与椭圆
与椭圆 交于不同的两点
交于不同的两点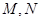 .
.
(1)求椭圆 的方程;
的方程;
(2)求 的取值范围.
的取值范围.
(1)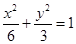 ;(2)
;(2)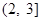
【解析】
试题分析:(1)由离心率为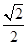 ,得
,得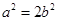 ,再根据椭圆C过点
,再根据椭圆C过点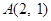 ,代入得
,代入得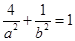 ,联立之可求得
,联立之可求得 的值,进而写出椭圆方程;(2)考察直线和椭圆的位置关系,一般要将直线方程和椭圆方程联立,得关于某一变量的一元二次方程,设交点,然后利用韦达定理达到设而不求的目的,同时要注意
的值,进而写出椭圆方程;(2)考察直线和椭圆的位置关系,一般要将直线方程和椭圆方程联立,得关于某一变量的一元二次方程,设交点,然后利用韦达定理达到设而不求的目的,同时要注意 的隐含条件,该题设直线方程为
的隐含条件,该题设直线方程为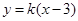 ,代入椭圆方程得
,代入椭圆方程得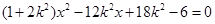 ,则
,则 >0,得
>0,得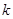 的范围,设交点
的范围,设交点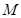
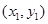 ,
,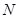
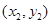 ,将
,将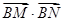 表示为
表示为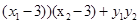 ,然后利用韦达定理将其表示为
,然后利用韦达定理将其表示为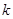 的式子,进而可以看成是自变量为
的式子,进而可以看成是自变量为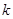 的函数
的函数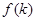 ,求其值域即可.
,求其值域即可.
试题解析:(1)由题意得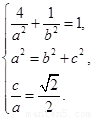 解得
解得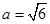 ,
,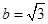 .
.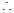 椭圆
椭圆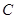 的方程为
的方程为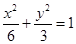 .
.
(2)由题意显然直线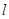 的斜率存在,设直线
的斜率存在,设直线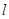 的方程为
的方程为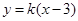 ,
,
由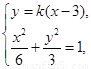 得
得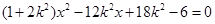 .
. 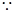 直线
直线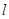 与椭圆
与椭圆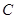 交于不同的两点
交于不同的两点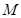 ,
,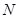 ,
,
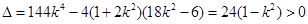 ,解得
,解得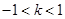 .设
.设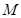 ,
,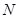 的坐标分别为
的坐标分别为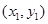 ,
,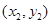 ,则
,则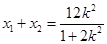 ,
,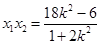 ,
,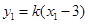 ,
,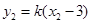 .
.
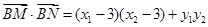
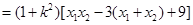
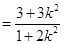
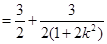 .
.
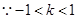 ,
,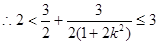 .
.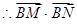 的取值范围为
的取值范围为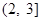 .
.
考点:1、椭圆的方程及简单几何性质;2、向量的数量积运算;3、韦达定理.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源:2012-2013学年山东省聊城市高三上学期1月份模块检测文科数学试卷(解析版) 题型:解答题
已知椭圆
 经过点
经过点 其离心率为
其离心率为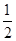 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设直线 与椭圆
与椭圆 相交于A、B两点,以线段
相交于A、B两点,以线段 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆 上,
上, 为坐标原点.求
为坐标原点.求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山西省、长治二中高三第二次联考文科数学 题型:解答题
(本小题满分12分)
已知椭圆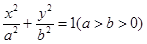 经过点
经过点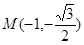 ,离心率为
,离心率为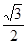 .
.
(1)求椭圆的方程;
(2)设过定点M(0,2)的直线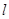 与椭圆交于不同的两点
与椭圆交于不同的两点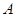 、
、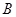 ,且
,且 为锐角(其中
为锐角(其中 为坐标原点),求直线
为坐标原点),求直线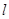 的斜率
的斜率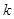 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年云南省高三9月月考文科数学 题型:解答题
(本小题满分12分)
已知椭圆
 经过点
经过点 其离心率为
其离心率为
(1)求椭圆 的方程
的方程
(2)设直线 与椭圆
与椭圆 相交于A、B两点,以线段
相交于A、B两点,以线段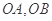 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆 上,
上, 为坐标原点. 求
为坐标原点. 求 到直线
到直线 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市海淀区高三下学期期中考试数学理卷 题型:解答题
(本小题共14分)
已知椭圆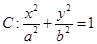
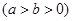 经过点
经过点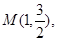 其离心率为
其离心率为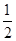 .
.
(Ⅰ)求椭圆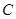 的方程;
的方程;
(Ⅱ)设直线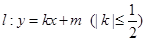 与椭圆
与椭圆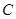 相交于A、B两点,以线段
相交于A、B两点,以线段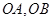 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆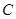 上,
上,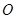 为坐标原点.求
为坐标原点.求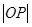 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com