
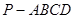 的底面与四个侧面的形状和大小如图所示。
的底面与四个侧面的形状和大小如图所示。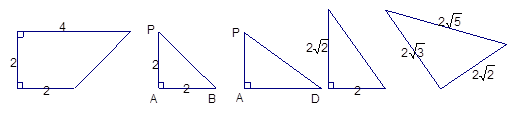
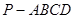 中四对线面垂直关系(不要求证明)
中四对线面垂直关系(不要求证明)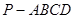 中,若
中,若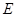 为
为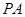 的中点,求证:
的中点,求证: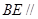 平面
平面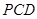
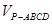 值。
值。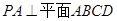 ,
,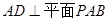 ,
,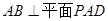 ,
,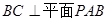
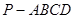 中,
中,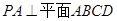 ,
,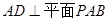 ,
,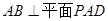 ,
,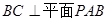 都是满足题意的线面垂直。
都是满足题意的线面垂直。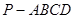 中,若
中,若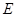 为
为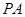 的中点,那么则有
的中点,那么则有 EF//AD,EF=
EF//AD,EF=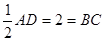
 中,
中, 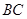 //
//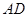
 四边形
四边形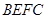 是平行四边形,即
是平行四边形,即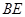 //
//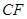
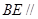 平面
平面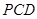
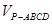 值,利用底面积乘以高的三分之一得到结论。
值,利用底面积乘以高的三分之一得到结论。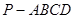 中,
中,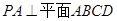 ,
,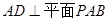 ,
, ,
, ………………………………4分 (只要对一个得一分)
………………………………4分 (只要对一个得一分)
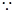 E,F分别是PA,PD的中点
E,F分别是PA,PD的中点 EF//AD,EF=
EF//AD,EF=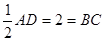 ……………………………6分
……………………………6分 中,
中,  //
//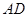
 四边形
四边形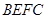 是平行四边形,即
是平行四边形,即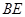 //
//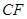
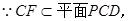
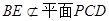 ……………………………………………8分
……………………………………………8分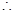
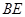 //
//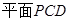 …………..9分
…………..9分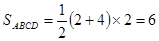 ,
, 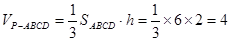
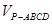 值为4……………………………………………………………….12分
值为4……………………………………………………………….12分

科目:高中数学 来源:不详 题型:解答题
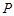 为斜三棱柱
为斜三棱柱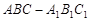 的侧棱
的侧棱 上一点,
上一点,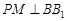 交
交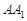 于点
于点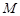 ,
,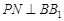 交
交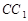 于点
于点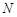 .
.
 ;
; 中有余弦定理:
中有余弦定理: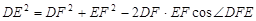 . 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式(只写结论,不必证明)
. 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式(只写结论,不必证明)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
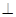 AD且AB=AD=
AD且AB=AD=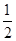 CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
CD=1,现以AD为一边向梯形外作正方形ADEF,然后沿AD将正方形翻拆,使平面ADEF与平面ABCD互相垂直如图(2)。
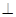 平面BEC
平面BEC查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
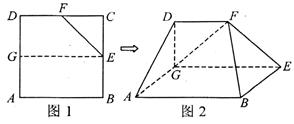
 与正三角形
与正三角形 所在平面互相垂直,M、Q分别是PC,AD的中点。
所在平面互相垂直,M、Q分别是PC,AD的中点。

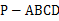 的体积
的体积 若存在,指出N的位置,若不存在,请说明理由。
若存在,指出N的位置,若不存在,请说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
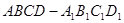 中,
中,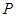 为正方形
为正方形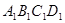 四边上的动点,
四边上的动点,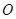 为底面正方形
为底面正方形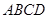 的中心,
的中心,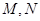 分别为
分别为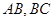 的中点,点
的中点,点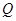 为平面
为平面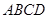 内一点,线段
内一点,线段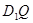 与
与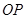 互相平分,则满足
互相平分,则满足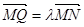 的实数
的实数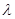 的值有( )
的值有( )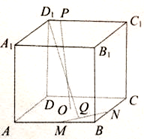
A.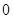 个 个 | B.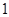 个 个 | C. 个 个 | D. 个 个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com