
已知正数数列 中,
中, ,前
,前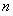 项和为
项和为 ,对任意
,对任意 ,
, 、
、 、
、 成等差数列.
成等差数列.
(1)求 和
和 ;
;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,当
,当 时,证明:
时,证明: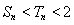 .
.
科目:高中数学 来源: 题型:
| an |
| an-1 |
| an-1+2n-1 |
| an-2n+1 |
| 1 | |||
|
| n |
| an(2n-1) |
| n2+cn |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| an+2 |
| 1 |
| an+2 |
| 7 |
| 10 |
查看答案和解析>>
科目:高中数学 来源:广东省深圳高级中学2011届高三高考前最后模拟数学文科试卷 题型:044
数列{an}的各项均为正数,Sn为其前n项和,对于任意n∈N*,总有an,Sn,![]() 成等差数列.
成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}的前n项和为Tn,且![]() ,求证:对任意实数x∈(1,e](e是常数,e=2.71828…)和任意正整数n,总有Tn<2;
,求证:对任意实数x∈(1,e](e是常数,e=2.71828…)和任意正整数n,总有Tn<2;
(Ⅲ)已知正数数列{cn}中,![]() ,求数列{cn}中的最大项.
,求数列{cn}中的最大项.
查看答案和解析>>
科目:高中数学 来源:2011年四川省宜宾市南溪一中高考数学一诊模拟试卷3(文科)(解析版) 题型:解答题
 ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;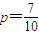 时,数列{bn}中是否存在最小项?若存在说明是第几项,如果不存在,说明理由.
时,数列{bn}中是否存在最小项?若存在说明是第几项,如果不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:2010年江西省南昌市新建二中高考数学二模试卷(文科)(解析版) 题型:解答题
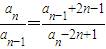 ,求
,求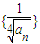 的前n项和为An,证明
的前n项和为An,证明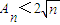 ;
;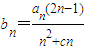 (c为非零常数),若数列{bn}是等差数列,其前n项和为Sn,求数列{(-1)nSn}的前m项和Tm.
(c为非零常数),若数列{bn}是等差数列,其前n项和为Sn,求数列{(-1)nSn}的前m项和Tm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com