
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 连接BD,与AC交于O点,取PD的中点E,连接OE,AE.运用中位线定理,可得∠AOE即为直线PB与直线AC所成角.运用线面垂直的性质和勾股定理,解三角形AOE,即可得到所求值.
解答 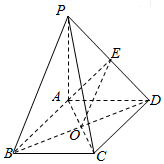 解:连接BD,与AC交于O点,取PD的中点E,连接OE,AE.
解:连接BD,与AC交于O点,取PD的中点E,连接OE,AE.
由中位线定理,可得OE∥PB,且OE=$\frac{1}{2}$PB,
即有∠AOE即为直线PB与直线AC所成角.
由PA⊥平面ABCD,设PA=AB=a,
可得直角三角形PAB中,PB=$\sqrt{2}$a,
OE=$\frac{\sqrt{2}}{2}$a,
在等腰直角三角形PAD中,AE=$\frac{1}{2}$PD=$\frac{\sqrt{2}}{2}$a,
在正方形ABCD中,AO=$\frac{1}{2}$AC=$\frac{\sqrt{2}}{2}$a,
则△AOE为等边三角形,
可得∠AOE=$\frac{π}{3}$.
故选:C.
点评 本题考查空间异面直线所成角的求法,注意运用三角形的中位线定理和解三角形的知识,考查线面垂直的性质和勾股定理的运用,属于基础题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
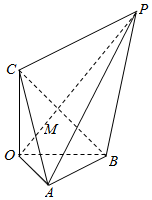 如图,已知三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直且OA=OB=OC,△ABC为等边三角形,M为△ABC内部一点,点P在OM的延长线上,且PA=PB.PA=$\sqrt{5}$OC,OP=$\sqrt{6}$OC.
如图,已知三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直且OA=OB=OC,△ABC为等边三角形,M为△ABC内部一点,点P在OM的延长线上,且PA=PB.PA=$\sqrt{5}$OC,OP=$\sqrt{6}$OC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2013×2014 | B. | 2013+2014 | C. | 20142 | D. | 20132 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,已知正方形ABCD的边长为1,E在CD延长线上,且DE=CD.动点P从点A出发沿正方形ABCD的边按逆进针方向运动一周回到A点,其中$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$,则下列命题正确的是①②.(填上所有正确命题的序号)
如图,已知正方形ABCD的边长为1,E在CD延长线上,且DE=CD.动点P从点A出发沿正方形ABCD的边按逆进针方向运动一周回到A点,其中$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$,则下列命题正确的是①②.(填上所有正确命题的序号)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com