
分析 (1)根据两角和的正弦公式化简解析式,由三角函数的周期公式求出f(x)的最小正周期,由正弦函数的增区间求出f(x)的单调递增区间;
(2)由x的范围求出$\frac{x}{2}+\frac{π}{3}$的范围,由正弦函数的最大值求出f(x)在$[0,\frac{π}{2}]$上的最值.
解答 解:(1)由题意得,$\left.\begin{array}{l}{f(x)=2(\frac{1}{2}sin\frac{x}{2}+\frac{\sqrt{3}}{2}cos\frac{x}{2})}\end{array}\right.$
=$\left.\begin{array}{l}{2(cos\frac{π}{3}sin\frac{x}{2}+sin\frac{π}{3}cos\frac{x}{2})}\end{array}\right.$=$\left.\begin{array}{l}{2sin(\frac{x}{2}+\frac{π}{3})}\end{array}\right.$,
由T=$\frac{2π}{ω}=\frac{2π}{\frac{1}{2}}=4π$得,f(x)的最小正周期是4π,
由$-\frac{π}{2}+2kπ≤\frac{x}{2}+\frac{π}{3}≤\frac{π}{2}+2kπ(k∈Z)$得,
$-\frac{5π}{3}+4kπ≤x≤\frac{π}{3}+4kπ(k∈Z)$,
∴f(x)的单调递增区间是$[-\frac{5π}{3}+4kπ,\frac{π}{3}+4kπ](k∈Z)$;
(2)∵$x∈[0,\frac{π}{2}]$,∴$\frac{x}{2}+\frac{π}{3}∈[\frac{π}{3},\frac{7π}{12}]$,
当$\frac{x}{2}+\frac{π}{3}=\frac{π}{2}$时,此时$\left.\begin{array}{l}{sin(\frac{x}{2}+\frac{π}{3})}\end{array}\right.$=1,
函数f(x)取到最大值是$f{(x)_{max}}=2\end{array}$,
当$\frac{x}{2}+\frac{π}{3}=\frac{π}{3}$时,此时$\left.\begin{array}{l}{sin(\frac{x}{2}+\frac{π}{3})}\end{array}\right.$=$\frac{\sqrt{3}}{2}$,
函数f(x)取到最小值是$f{(x)}_{min}=\sqrt{3}$.
点评 本题考查正弦函数的图象与性质,三角函数周期公式,以及两角和的正弦公式,考查化简、变形能力.


科目:高中数学 来源: 题型:选择题
| A. | 点O在圆外 | B. | 点O在圆上 | C. | 点O在圆内 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 将三项式(x2+x+1)n展开,当n=0,1,2,3,…时,得到以下等式:
将三项式(x2+x+1)n展开,当n=0,1,2,3,…时,得到以下等式:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 1 | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
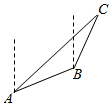 一艘海轮从A出发,沿北偏东75°的方向航行(2$\sqrt{3}$-2)nmile到达海岛B,然后从B出发,沿北偏东15°的方向航行4nmile到达海岛C.
一艘海轮从A出发,沿北偏东75°的方向航行(2$\sqrt{3}$-2)nmile到达海岛B,然后从B出发,沿北偏东15°的方向航行4nmile到达海岛C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com