
分析 由x的范围,化简f(x)=1+a,由恒成立思想可得a≤x+2的最小值,运用一次函数的单调性,可得最小值,解不等式即可得到a的范围.
解答 解:当x∈[-$\frac{a}{2}$,$\frac{1}{2}$]时,f(x)=|2x-1|+|2x+a|=1-2x+2x+a=1+a,
由a>-1,当x∈[-$\frac{a}{2}$,$\frac{1}{2}$]时,f(x)≤g(x),
即为1+a≤x+3,即a≤x+2,
由x∈[-$\frac{a}{2}$,$\frac{1}{2}$],可得x+2∈[2-$\frac{a}{2}$,$\frac{5}{2}$],
即有a≤2-$\frac{a}{2}$,解得-1<a≤$\frac{4}{3}$.
则a的取值范围是(-1,$\frac{4}{3}$].
故答案为:(-1,$\frac{4}{3}$].
点评 本题考查含绝对值函数的化简和运用,考查不等式恒成立问题的解法,注意运用转化思想,及参数分离和函数的单调性求最值,考查运算能力,属于中档题.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2] | B. | (-∞,1) | C. | [2,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
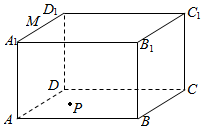 如图,长方体ABCD-A1B1C1D1,AB=BC=2,AA1=$\sqrt{3}$,M为A1D1的中点,P为底面四边形ABCD内的动点,且满足PM=PC,则点P的轨迹的长度为( )
如图,长方体ABCD-A1B1C1D1,AB=BC=2,AA1=$\sqrt{3}$,M为A1D1的中点,P为底面四边形ABCD内的动点,且满足PM=PC,则点P的轨迹的长度为( )| A. | $\sqrt{3}$ | B. | 3 | C. | $\frac{2π}{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com