练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

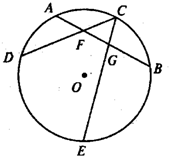
    如图．过⊙O的弧AB的中点C作弦CD，CE分别与AB相交于点F，G．
    求证：CD•CF=CE•CG．

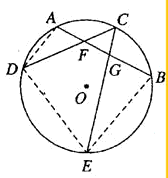    证明：连接AD，DE，EB，
    由A，D，E，B四点共圆，得∠ADE+∠B=180°
    ∵∠ADE=∠ADC+∠CDE
    ∴∠ADC+∠CDE+∠B=180°①
    ∵点C是弧AB的中点，
    ∴∠ADC=∠BEC ②
    由①②，得∴∠BEC+∠CDE+∠B=180°，即（∠BEC+∠B）+∠CDE=180°，∴∠EGA+∠CDE=180°，则四边形DFEG内接于圆
    ∵直线CFD，CGE是该圆的两条割线
    ∴CD×CF=CG×CE
    分析：分析知，若能证明四点DFGE共圆，则可以有割线定理证得CD•CF=CE•CG，由北证明目标确定，在图形中连接DE，证明四点共圆即可．
    点评：本题考查与圆有关的比例线段，解本题的关键是由所证的结论观察出其成立的等价条件四点DFGE共圆，在几何证明中确定好解决问题的方向对顺利解题很关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网附加题：
    A．如图，四边形ABCD内接于圆O，弧AB=弧AD，过A点的切线交CB的延长线于E点．
    求证：AB2=BE•CD．
    B．设数列{an}，{bn}满足an+1=3an+2bn，bn+1=2bn，且满足
    an+4
    bn+4
    =M
    an
    bn
    ，试求二阶矩阵M．
    C．已知椭圆C的极坐标方程为ρ2=
    12
    3cos2θ+4sin2θ
    ，点F1，F2为其左、右焦点，直线l的参数方程为
    x=2+
    		2
    2
    t
    y=
    		2
    2
    t
    （t为参数，t∈R）．求点F1，F2到直线l的距离之和．
    D．已知x，y，z均为正数．求证：
    x
    yz
    +
    y
    zx
    +
    z
    xy
    ≥
    1
    x
    +
    1
    y
    +
    1
    z
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

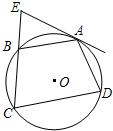    精英家教网A．如图，四边形ABCD内接于⊙O，弧AB=弧AD，过A点的切线交CB的延长线于E点．
    求证：AB2=BE•CD．
    B．已知矩阵M
    2-3
    1-1
    所对应的线性变换把点A（x，y）变成点A′（13，5），试求M的逆矩阵及点A的坐标．
    C．已知圆的极坐标方程为：ρ2-4
    		2
    ρcos(θ-
    π
    4
    )+6=0    ．
    （1）将圆的极坐标方程化为直角坐标方程；
    （2）若点P（x，y）在该圆上，求x+y的最大值和最小值．
    D．解不等式|2x-1|＜|x|+1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    22、如图．过⊙O的弧AB的中点C作弦CD，CE分别与AB相交于点F，G．
    求证：CD•CF=CE•CG．

    查看答案和解析>>

    科目：高中数学 来源：2010年江苏省泰州高级中学高考数学模拟试卷（解析版） 题型：解答题

    附加题：
    A．如图，四边形ABCD内接于圆O，弧AB=弧AD，过A点的切线交CB的延长线于E点．
    求证：AB2=BE•CD．
    B．设数列{an}，{bn}满足an+1=3an+2bn，bn+1=2bn，且满足=M，试求二阶矩阵M．
    C．已知椭圆C的极坐标方程为，点F1，F2为其左、右焦点，直线l的参数方程为（t为参数，t∈R）．求点F1，F2到直线l的距离之和．
    D．已知x，y，z均为正数．求证：．

    查看答案和解析>>

    同步练习册答案