
 是定义在
是定义在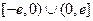 上的奇函数,当
上的奇函数,当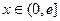 ,
, (其中
(其中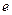 是自然对数的底,
是自然对数的底,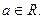 )
) 的解析式;
的解析式;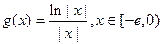 ,求证:当
,求证:当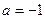 时,
时,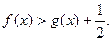
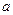 ,使得当
,使得当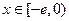 时,
时, 的最小值是3?如果存在,求出实数
的最小值是3?如果存在,求出实数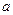 的值;如果不存在,请说明理由。
的值;如果不存在,请说明理由。
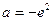 ,使得
,使得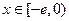 时,
时, 有最小值3
有最小值3
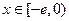 ,则
,则
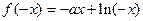
 是
是 定义在
定义在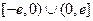 上的奇函数,
上的奇函数,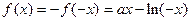 …………2分
…………2分 的解析式为
的解析式为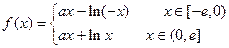 ……3分
……3分 (2)证明:当
(2)证明:当
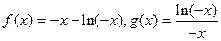
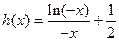
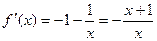
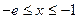 时,
时,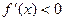
 单调递减…………5分
单调递减…………5分
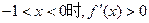 ,此时
,此时 单调递增
单调递增 的最小值为
的最小值为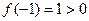
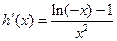
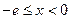 时,
时,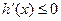 ,此时
,此时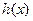 单调递减
单调递减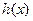 的最大值为
的最大值为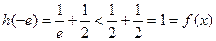 的最小值
的最小值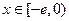 时,
时,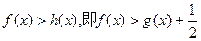 …………8分
…………8分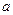 ,使得当
,使得当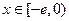 ,时,
,时,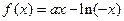 有最小值为3
有最小值为3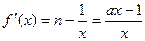 …………9分
…………9分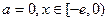 时,
时,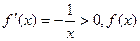 在区间
在区间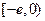 单调递增,
单调递增, 最小值为
最小值为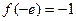 ,不满足最小值是3
,不满足最小值是3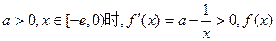 在区间
在区间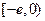 上单调递增,
上单调递增, 的最小值是
的最小值是 ,也不满足最小值3
,也不满足最小值3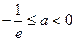 ,
,
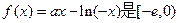 增函数。
增函数。 的最小值为
的最小值为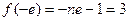 ,解得
,解得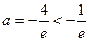 (舍去)
(舍去) 时,
时, ,此时函数
,此时函数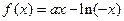
 是减函数
是减函数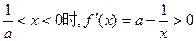 ,
,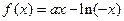 是减函数
是减函数 的最小值为
的最小值为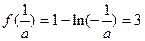 ,解得
,解得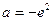 ……611
……611 分
分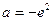 ,使得
,使得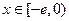 时,
时, 有最小值3…………12分
有最小值3…………12分

科目:高中数学 来源:不详 题型:解答题
 设备,进行该
设备,进行该 产品的生产加工.已知生产这种产品每件还需成本费40元,经过市场调研发现:该产品的销售单价定在100元到300元之间较为合理.当销售单价定为100元时,年销售量为20万件;当销售单价超过100元,但不超过200元时,每件产品的销售价格每增加10元,年销售量将减少0.8万件;当销售单价超过200元,但不超过300元时,每件产品的销售价格在200元的基础上,每增加10元,年销售量将再减少1万件.设销售单价为
产品的生产加工.已知生产这种产品每件还需成本费40元,经过市场调研发现:该产品的销售单价定在100元到300元之间较为合理.当销售单价定为100元时,年销售量为20万件;当销售单价超过100元,但不超过200元时,每件产品的销售价格每增加10元,年销售量将减少0.8万件;当销售单价超过200元,但不超过300元时,每件产品的销售价格在200元的基础上,每增加10元,年销售量将再减少1万件.设销售单价为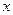 (元),年销售量为
(元),年销售量为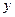 (万件),年获利为
(万件),年获利为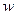 (万元).
(万元).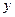 与
与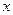 之间的函数关系式;
之间的函数关系式;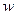 与
与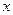 之间的函数关系式,并说明投资的第一年,该公司是赢利还
之间的函数关系式,并说明投资的第一年,该公司是赢利还 是亏损?若赢利,最大利润是多少?若亏损,最少亏损是多少?(=1521)
是亏损?若赢利,最大利润是多少?若亏损,最少亏损是多少?(=1521)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com