
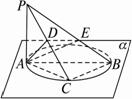
①∠AED是二面角A—PB—C的平面角;
②∠ACD是二面角P—BC—A的平面角;
③∠EDA是二面角A—PC—B的平面角;
④∠BAC是二面角B—PA—C的平面角;
⑤∠PAC是二面角P—AB—C的平面角.
其中正确结论的序号是____________________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2012年人教A版高中数学必修四2.3平面向量基本定理及坐标表示(一)(解析版) 题型:填空题
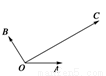
如图所示,平面内有三个向量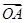 、
、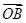 、
、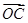 ,其中
,其中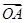 与
与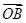 的夹角为120°,
的夹角为120°,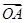 与
与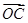 的夹角为30°,且|
的夹角为30°,且|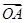 |=|
|=|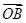 |=1,|
|=1,|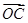 |=2
|=2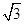 .若
.若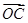 =λ
=λ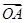 +μ
+μ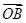 (λ,μ∈R),则λ+μ的值为______.
(λ,μ∈R),则λ+μ的值为______.
查看答案和解析>>
科目:高中数学 来源:2013届福建省高二下学期期中文科数学试卷(解析版) 题型:填空题
现有一个关于平面图形的命题,如图所示,同一个平面内有两个边长都是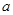 的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为
的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为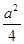 .类比到空间,有两个棱长均为
.类比到空间,有两个棱长均为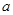 的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为_ .
的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为_ .

查看答案和解析>>
科目:高中数学 来源:2013届福建师大附中高二下学期期中理科数学试卷(解析版) 题型:填空题
现有一个关于平面图形的命题,如图所示,同一个平面内有两个边长都是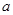 的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为
的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为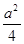 .类比到空间,有两个棱长均为
.类比到空间,有两个棱长均为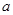 的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .

查看答案和解析>>
科目:高中数学 来源: 题型:
(1)当![]() 取最小值时,求
取最小值时,求![]() 的坐标;
的坐标;
(2)当点M满足(1)的条件和结论时,求∠AMB的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com