
分析 (Ⅰ)分别解出关于对数函数、二次函数的不等式,取交集即可;(Ⅱ)根据p是q的充分必要条件,得到关于a的不等式组,解出即可.
解答 解:(Ⅰ)由${log}_{\frac{1}{3}}^{x}$>-1,解得:0<x<3,
由x2-6x+8<0,解得:2<x<4,
综上:2<x<3;
(Ⅱ)由(Ⅰ)得:p:2<x<3,
命题q:实数x满足不等式2x2-9x+a<0,
解不等式得:$\frac{a-\sqrt{81-8a}}{4}$<x<$\frac{a+\sqrt{81-8a}}{4}$,
由p是q的充分条件,
得$\left\{\begin{array}{l}{\frac{a-\sqrt{81-8a}}{4}≤2}\\{\frac{a+\sqrt{81-8a}}{4}≥3}\end{array}\right.$,解得:7≤a≤8.
点评 本题考查了解不等式组问题,考查充分必要条件,是一道基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
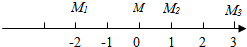 三台机器人位于同一直线上(如图所示),它们所生产的零件必须逐一送到一个检验台上,经检验合格后,才能送到下一道工序继续加工,已知机器人M1的工作效率是机器人M2的2倍,机器人M2的工作效率是机器人M3的3倍,问检验台放何处最好?(即各机器人到检验台所走距离的总和最小)
三台机器人位于同一直线上(如图所示),它们所生产的零件必须逐一送到一个检验台上,经检验合格后,才能送到下一道工序继续加工,已知机器人M1的工作效率是机器人M2的2倍,机器人M2的工作效率是机器人M3的3倍,问检验台放何处最好?(即各机器人到检验台所走距离的总和最小)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com