练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f(x)＝，g(x)＝x2＋x＋1，求f[g(2)]和g[f(2)]的值．

    答案：
    解析：

    　　解：f[g(2)]＝f(7)＝，g[f(2)]＝g()＝．

    　　点评：学生对这类问题的求解，开始的时候有点难，但随着对函数定义的理解，这类问题的解决就比较容易了．


    提示：

    这是一个求函数值的问题，它分为两层，从里层开始计算，一层一层地计算，实际上就是按照函数的定义来进行分解．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：高三数学教学与测试 题型：013

    已知f(x)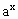＝，g(x)＝－，且lga＋lgb＝0，a≠1，b≠1．则y＝f(x)与y＝g(x)的图象

    [　　]

    A．关于直线x＋y＝0对称

    B．关于直线x－y＝0对称

    C．关于y轴对称

    D．关于原点对称

    查看答案和解析>>

    科目：高中数学 来源：2004全国各省市高考模拟试题汇编(天利38套)·数学 题型：013

    已知f(x)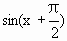＝，g(x)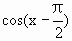＝，则下列结论中正确的是

    [　　]

    A．函数y＝f(x)·g(x)的周期为2π

    B．函数y＝f(x)·g(x)的最大值为1

    C．将f(x)的图像向左平移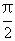单位后得g(x)的图像

    D．将f(x)的图像向右平移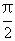单位后得g(x)的图像

    查看答案和解析>>

    科目：高中数学 来源：上海市进才中学2007届高三文科月考六数学试题 题型：038

    已知f(x)＝及g(x)＝．

    (1)求f(x)、g(x)的定义域及f(x)·g(x)的值；

    (2)指出函数f(x)的单调性，并求函数f(x)的最小值；

    (3)若a＝，b＝t，c＝x＋1，是否存在满足下列条件的正数t，使得对于任意的正数x，a、b、c都可以成为某个三角形三边的长？若存在，则求出t的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f(x)＝，g(x)＝x2＋2.

    (1)求f(2)，g(2)的值；

    (2)求f(g(2))的值；

    (3)求f(g(x))的解析式．

    查看答案和解析>>

    同步练习册答案