
分析 根据条件xf'(x)+2f(x)=$\frac{1}{x^2}$构造函数F(x)=x2f(x)-lnx,通过对导数的分析,得出F(x)为常数函数,进而求得f(x)的解析式,再运用导数求该函数的最大值.
解答 解:构造函数F(x)=x2f(x)-lnx,且F(1)=12f(1)-ln1=1,
则F'(x)=x2f'(x)+2xf(x)-$\frac{1}{x}$=x[xf'(x)+2f(x)-$\frac{1}{x^2}$],
∵xf'(x)+2f(x)=$\frac{1}{x^2}$,
∴F'(x)=0恒成立,即F(x)为常数函数,
由于F(1)=1,所以F(x)=x2f(x)-lnx=1,
分离f(x)得,f(x)=$\frac{1+lnx}{x^2}$,令f'(x)=-$\frac{1+2lnx}{x^3}$=0,解得x=${e}^{-\frac{1}{2}}$,
且x∈(0,${e}^{-\frac{1}{2}}$),f'(x)>0,x∈(${e}^{-\frac{1}{2}}$,+∞),f'(x)<0,
所以,x∈(0,${e}^{-\frac{1}{2}}$)函数递增,(${e}^{-\frac{1}{2}}$,+∞)单调递减,
所以,f(x)max=f(x)极大值=f(${e}^{-\frac{1}{2}}$)=$\frac{e}{2}$,
故填:$\frac{e}{2}$.
点评 本题主要考查了导数的运算,并运用导数研究函数的单调性和单调区间,求函数最值,合理构造函数是解决本题的关键,属于难题.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{2}{3},+∞)$ | B. | (1,+∞) | C. | $[{\frac{2}{3},1}]$ | D. | $(\frac{2}{3},\left.1]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
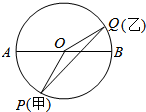 如图,有一个半径为20m的圆形水池,甲、乙两人分别从水池一条直径AB的两端开始,同时按逆时针方向绕水池边缘做匀速圆周运动,已知乙绕水池2圈需要1min,甲的速度是乙的两倍.如果从两人出发时开始计时,求当乙绕水池1周的过程中,两人的直线距离l(m)和时间t(s)的函数关系式.
如图,有一个半径为20m的圆形水池,甲、乙两人分别从水池一条直径AB的两端开始,同时按逆时针方向绕水池边缘做匀速圆周运动,已知乙绕水池2圈需要1min,甲的速度是乙的两倍.如果从两人出发时开始计时,求当乙绕水池1周的过程中,两人的直线距离l(m)和时间t(s)的函数关系式.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com