【答案】
分析:由已知中圆的标准方程可以求出圆心坐标及半径,结合直线l被圆所截弦长,根据半弦长,弦心距,半径构造直角三角形,满足勾股定理,求出弦心距,分直线l的斜率不存在和直线l的斜率存在两种情况分类讨论,最后综合讨论结果,可得答案.
解答:解:∵圆(x-2)
2+y
2=4的半径为2
若AB=2
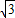
,
则圆心(2,0)到直线l距离d=1,
若直线l的斜率不存在,即x=-3,
此时圆心(2,0)到直线l距离为5不满足条件
若直线l的斜率存在,则可设直线l的方程为y-3=k(x-3)
即kx-y-3k+3=0
则d=
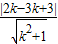
=1
解得k=

此时直线l的方程为y-3=

(x-3)
化为一般式可得4x-3y-3=0
综上直线l的方程是y=3或4x-3y-3=0
故答案为:y=3或4x-3y-3=0
点评:本题考查的知识点是直线与圆的位置关系,其中根据半弦长,弦心距,半径构造直角三角形,满足勾股定理,求出弦心距,是解答的关键.

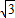 ,则直线l的方程是 .
,则直线l的方程是 . 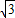 ,
,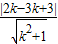 =1
=1
 (x-3)
(x-3)

 名校课堂系列答案
名校课堂系列答案