
科目:高中数学 来源: 题型:
已知椭圆
 的离心率为
的离心率为 ,长轴长为
,长轴长为 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设 为椭圆C的右焦点,T为直线
为椭圆C的右焦点,T为直线 上纵坐标不为
上纵坐标不为 的任意一点,过
的任意一点,过 作
作 的垂线交椭圆C于点P,Q.
的垂线交椭圆C于点P,Q.
(ⅰ)若OT平分线段PQ(其中O为坐标原点),求 的值;
的值;
(ⅱ)在(ⅰ)的条件下,当 最小时,求点T的坐标.
最小时,求点T的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列四个判断
①函数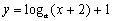 的图象过定点(-1,2) ②若函数
的图象过定点(-1,2) ②若函数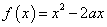 在
在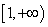 上是增函数,则
上是增函数,则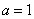 ;③方程
;③方程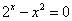 有两个不等的根.④函数
有两个不等的根.④函数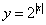 的最小值是1.其中不正确的序号是____________
的最小值是1.其中不正确的序号是____________
查看答案和解析>>
科目:高中数学 来源: 题型:
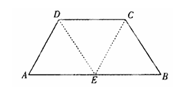
如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点.将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为( )
A.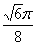 B.
B.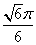 C.
C.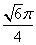 D.
D.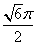
查看答案和解析>>
科目:高中数学 来源: 题型:
某家电产品受在保修期内维修费等因素的影响,企业生产每件的利润与该产品首次出现故障的时间有关.某厂家生产甲、乙两种品牌,保修期均为2年.现从该厂已售出的两种品牌家电中各随机抽取50件,统计数据如下:
| 品牌 | 甲 | 乙 | |||
| 首次出现故障时间x(年) | 0<x≤1 | 1<x≤2 | x>2 | 0<x≤2 | x>2 |
| 数量(件) | 2 | 3 | 45 | 5 | 45 |
| 每件利润(百元) | 1 | 2 | 3 | 1.8 | 2.9 |
将频率视为概率,解答下列问题:
(I)从该厂生产的甲、乙品牌产品中随机各抽取一件,求其至少有一件首次出现故障发生在保修期内的概率;
(II)若该厂生产的家电均能售出,记生产一件甲品牌的利润为X1,生产一件乙品牌家电的利润为X2,分别求X1,X2的分布列;
(III)该厂预计今后这两种品牌家电销量相当,由于资金限制,只能生产其中一种品牌的家电.若从经济效益的角度考虑,你认为应生产哪种品牌的家电?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com