Question

一个截面为抛物线形的旧河道,河口宽AB=4 m ,河深2 m ,现要将其截面改造为等腰梯形,要求河道深度不变,而且施工时只能挖土,不准向河道填土,试求当截面梯形的下底长为多少米时,才能使挖出的土最少?

Answer 1

解析：此题是一道实际应用问题,要将截面改造为等腰梯形,又要使所挖出的土最少,只能沿着抛物线上某一点的切线去挖.?

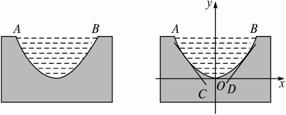
如图,以抛物线顶点为原点,AB中垂线为y轴,建立直角坐标系,则A(-2,2),B(2,2).?

设抛物线方程:x²=2py(p＞0),将点B(2,2)代入得p=1 ,?

所以抛物线方程为x²=2y,即y=x².?

设等腰梯形的腰与抛物线相切于点P(t, t²),?

则过点P的切线l的斜率为y′|_x=t=t,?

所以一腰的方程为y-=t(x-t),?

即y=tx-.?

当y=0时,x=;y=2时,x=+.?

所以截面面积S=,当且仅当t=,即t=2时,“=”成立,此时下底边长为.

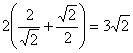答案：当截面梯形的下底面边长为m时,挖出的土最少.