
 .
. .
. ,由于x>0时,f(x)<0得出
,由于x>0时,f(x)<0得出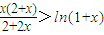 ,考察发现,若取x=
,考察发现,若取x=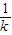 ,则可得出
,则可得出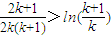 ,以此为依据,利用放缩法,即可得到结论
,以此为依据,利用放缩法,即可得到结论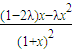 ,且f′(0)=0…3分
,且f′(0)=0…3分 ,则当0<x<2(1-2λ)时,f′(x)>0,所以当0<x<2(1-2λ)时,f(x)>0,
,则当0<x<2(1-2λ)时,f′(x)>0,所以当0<x<2(1-2λ)时,f(x)>0, ,则当x>0时,f′(x)<0,所以当x>0时,f(x)<0
,则当x>0时,f′(x)<0,所以当x>0时,f(x)<0 …6分
…6分 ,由(I)知,当x>0时,f(x)<0,即
,由(I)知,当x>0时,f(x)<0,即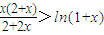
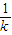 ,则
,则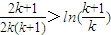 …9分
…9分 =
=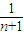 +
+ +…+
+…+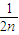 +
+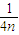
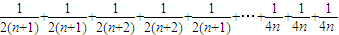
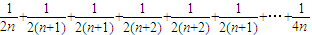
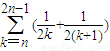
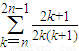 >
> =ln2n-lnn=ln2
=ln2n-lnn=ln2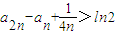 …12分
…12分

科目:高中数学 来源:2013-2014学年四川省绵阳市高三12月月考理科数学试卷(解析版) 题型:解答题
已知函数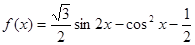 ,
,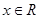
(I)若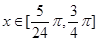 ,求函数
,求函数 的最大值和最小值,并写出相应的x的值;
的最大值和最小值,并写出相应的x的值;
(II)设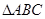 的内角
的内角 、
、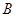 、
、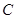 的对边分别为
的对边分别为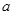 、
、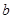 、
、 ,满足
,满足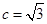 ,
,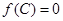 且
且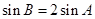 ,求
,求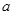 、
、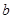 的值
的值
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省省城名校高三第一次联考数学试卷(理科)(解析版) 题型:解答题
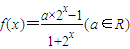 .
.查看答案和解析>>
科目:高中数学 来源:2010年北京市宣武区高考数学一模试卷(理科)(解析版) 题型:解答题
 .
.查看答案和解析>>
科目:高中数学 来源:2013年山东省临沂市高考数学一模试卷(理科)(解析版) 题型:解答题
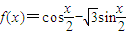 .
.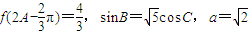 ,求△ABC的面积.
,求△ABC的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com