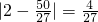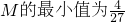Question

已知函数f（x）=-x³-2ax²-a²x+1-a（其中a＞-2）的图象在x=2处的切线与直线5x+y-12=0平行．
（1）求实数a的值及该切线方程；
（2）若对于任意的x₁，x₂∈[0，1]，|f（x₁）-f（x₂）|≤M恒成立，求实数M的最小值．

Answer 1

解：（1）由f（x）=-x³-2ax²-a²x+1-a得f'（x）=-3x²-4ax-a²
由题意f'（x）=-5，∴-3×4-8a-a²=-5即a²+8a+7=0
解得a=-1或a=-7，∵a＞-2，∴a=-1
∴f（x）=-3x³+2x²-x+2，∴f（2）=0
切线方程为：y=-5（x-2）即5x+y-10=0
（2）由（1）知f'（x）=-3x²+4x-1，令
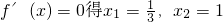
当x变化时f'（x），f（x）随x变化的情况如下表

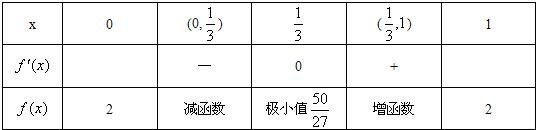
由表可知f（x）在区间[0，1]上的最小值，
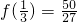
最大值为f（0）=f（1）=2
∵对任意的x₁，x₂∈[0，1]，f（x）=
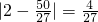
∵|f（x₁）-f（x₂）|≤M恒成立，
∴
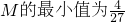
分析：（1）求出f（x）的导函数，因为切线与直线5x+y-12=0平行得到两条直线斜率相等，得到切线的斜率为-5即f'（2）=-5，解出a即可，且得到f（2）=0，然后写出切线方程即可；
（2）求出f'（x）=0时x的值，利用x的值找出范围讨论函数的增减性求出函数的最值，利用最大值减最小值得到M的最小值．
点评：考查学生理解函数恒成立的条件，理解导数的几何意义，以及利用导数求函数最值的能力．
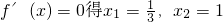
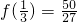