
����Ŀ������һ���ڼ䣬���������̳��ֱ�չ�����.
�����̳��Ĺ����ǣ���������100Ԫ���ɳ齱һ�Σ���װ�д�С����״��ͬ��4������4������Ĵ�������4�����н�������±���
�����Ľ�� | ��ý��𣨵�λ��Ԫ�� |
4�������4������ | 200 |
3������1�������3������1������ | 20 |
2������2������ | 10 |
��![]() Ϊ�齱һ�λ�õĽ�����
Ϊ�齱һ�λ�õĽ�����![]() �ķֲ��к�����.
�ķֲ��к�����.
�������̳��Ĺ����ǣ���������100Ԫ���ɳ齱10��.���У���![]() �γ齱�����ǣ��ӱ��Ϊ
�γ齱�����ǣ��ӱ��Ϊ![]() �Ĵ��У�װ�д�С����״��ͬ��
�Ĵ��У�װ�д�С����״��ͬ��![]() �������
�������![]() ����������
����������![]() ������������
�������ô�������![]() ������ɫ����ͬ����ɻ�ý���
������ɫ����ͬ����ɻ�ý���![]() Ԫ���ǵ�
Ԫ���ǵ�![]() �λ���
�λ���![]() .����������Ľ������Ӱ�죬��������õ��ܽ���Ϊ10�ν���֮��.
.����������Ľ������Ӱ�죬��������õ��ܽ���Ϊ10�ν���֮��.
����֤��![]() ��
��
����ij�˿���120Ԫ����Ʒ���������������أ��ӻ�ý����������������Ӧ��ѡ����һ���̳���
���𰸡����ֲ��м�����������Ϊ20����������֤������������ѡ����̳�.
��������
������![]() �����п�����ֵΪΪ200��20��10���ֱ�������ʣ��ɴ������
�����п�����ֵΪΪ200��20��10���ֱ�������ʣ��ɴ������![]() �ķֲ��к�������
�ķֲ��к�������
����������![]() ��2��3��
��2��3��![]() ��
��![]() ��
Ϊ��![]() �γ齱��õĽ���
�γ齱��õĽ���![]() ��ȡֵΪ
��ȡֵΪ![]() ��0�����
��0�����![]() ����֤��
����֤��![]() ������
������![]() �����ڼ��̳��齱�ý��������ֵ���ߣ���ѡ���̳���
�����ڼ��̳��齱�ý��������ֵ���ߣ���ѡ���̳���
������![]() �����п�����ֵΪΪ200��20��10��
�����п�����ֵΪΪ200��20��10��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
����������![]() ��2��3��
��2��3��![]() ��
��![]() ��
Ϊ��![]() �γ齱��õĽ���
�γ齱��õĽ���![]() ��ȡֵΪ
��ȡֵΪ![]() ��0��
��0��
��![]() ��
��
��![]() ��
��
����![]()
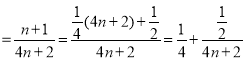 .
.
����![]() �ڶ������ڵ����ݼ�������
�ڶ������ڵ����ݼ�������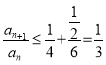 .
.
����![]() ��
��
�������![]() ��
��![]() ��2��3��
��2��3��![]() ��10��
��10��
��![]() Ϊ�����̳��齱��õ��ܽ�����
Ϊ�����̳��齱��õ��ܽ�����![]() ��
��
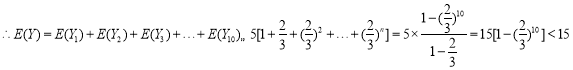
![]() �����ڼ��̳��齱�ý��������ֵ���ߣ���ѡ���̳���
�����ڼ��̳��齱�ý��������ֵ���ߣ���ѡ���̳���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������ͬʱ��ҵ����һ���ȫ�����۶�Ϊa��Ԫ�����ھ�Ӫ��ʽ��ͬ���׳���ǰn��������۶�Ϊ![]() (n2��n��2)��Ԫ���ҳ��е�n������۶��ǰһ�����۶��a
(n2��n��2)��Ԫ���ҳ��е�n������۶��ǰһ�����۶��a![]() ��Ԫ��
��Ԫ��
(1)��ס��������е�n�����۶�ı���ʽ��
(2)������ijһ���е������۶����һ���е������۶��50%����ó��н�����һ�����չ����ж���һ�����п��ܱ��չ�������������������������ڵڼ��ꣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() .
.
(��) ������![]() �ڵ�
�ڵ�![]() �������߷��̣�
�������߷��̣�
(��) ���ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
(��) ��![]() ,��
,��![]() ʱ,���������
ʱ,���������![]() ������
������![]() ��ʹ��
��ʹ��![]() ��
��![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ͨ����������ķ��������100������ij����ˮ������λ��t����Ƶ�ʷֲ�ֱ��ͼ��
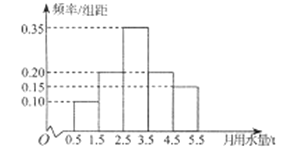
��������100�����������ˮ����ƽ��ֵ��
���Ӹ�����ˮ����![]() ��
��![]() ����������û��У��÷ֲ�����ķ�������5���Ļ�����5�˲μ�ˮ�۵���������֤�ᣬ�ִ���5�������ѡȡ2���ڻ��Ͻ��г������ԣ���ѡȡ��2�˾�������ˮ������2.5t���û��ĸ���.
����������û��У��÷ֲ�����ķ�������5���Ļ�����5�˲μ�ˮ�۵���������֤�ᣬ�ִ���5�������ѡȡ2���ڻ��Ͻ��г������ԣ���ѡȡ��2�˾�������ˮ������2.5t���û��ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ����Ϊ
����Ϊ![]() ���ҽ���Ϊ
���ҽ���Ϊ![]() ��ֱ��
��ֱ��![]() ��
��![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() ����
����![]() ��
��![]() ���е�.
���е�.
��������Բ�������ʣ�
������![]() ��ֱ������Բ�ཻ��
��ֱ������Բ�ཻ��![]() ���㣬
���㣬![]() ����
����![]() ���Ϸ�������
���Ϸ�������![]() ��
��![]() ֮�䣬��
֮�䣬��![]() ��ֱ��
��ֱ��![]() �ľ�����
�ľ�����![]() ��ֱ��
��ֱ��![]() �����
�����![]() ��.
��.
�ټ�![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ����
����![]() ��
��
����ԭ��![]() ��ֱ��
��ֱ��![]() �ľ���Ϊ
�ľ���Ϊ![]() ������Բ����.
������Բ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f��x����asin2x+bcos2x��a��b��R��ab��0������f��x��![]() ��һ��x��R��������������½��ۣ�
��һ��x��R��������������½��ۣ�
��![]() ��
��
��![]() ��
��
��f��x���ĵ�������������![]() ��
��
�ܺ���y��f��x���Ȳ����溯��Ҳ����ż������
�ݴ��ھ����㣨a��b����ֱ���뺯��f��x����ͼ���ཻ��������ȷ����Ϊ_____
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������УP��ABCD�У�����ABCD�����Σ���BAD��60�����߳�Ϊ4������PAD����ƽ����ƽ��ABCD��ֱ����E��AD���е㣬��Q�Dz���PC���е㣮

��1��������P��ABCD�������
��2����֤��PA��ƽ��BDQ��
��3�����߶�AB���Ƿ���ڵ�F��ʹֱ��PF��ƽ��PAD���ɵĽ�Ϊ30���������ڣ����AF�ij����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
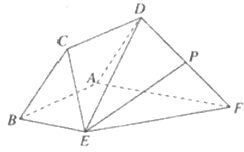
����Ŀ����ͼ����֪����![]() ��ֱ������
��ֱ������![]() ���ڵ�ƽ�滥�ഹֱ������
���ڵ�ƽ�滥�ഹֱ������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ���е�
���е�
������֤��![]() ��
��
����������![]() ������ֵ��
������ֵ��
������![]() Ϊ�߶�
Ϊ�߶�![]() ��һ�㣬
��һ�㣬![]() ����ֱ��
����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵΪ
���ɽǵ�����ֵΪ![]() ����
����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
(��)����![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() �������߷���.
�������߷���.
(��)��![]() ��
��![]() ������
������![]() ���������
���������![]() �����ֵ��
�����ֵ��
(��)��![]() ʱ��֤����
ʱ��֤����![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com