
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=BC=BB1 , AB1∩A1B=E,D为AC上的点,B1C∥平面A1BD. 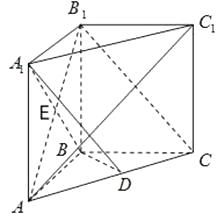
(1)求证:BD⊥平面A1ACC1;
(2)若AB=1,且ACAD=1,求二面角B﹣A1D﹣B1的余弦值.
【答案】
(1)证明:连结ED,
∵平面AB1C∩平面A1BD=ED,B1C∥平面A1BD,
∴B1C∥ED,
∵E为AB1中点,∴D为AC中点,
∵AB=BC,∴BD⊥AC①,
法一:由A1A⊥平面ABC,BD平面ABC,得A1A⊥BD,②,
由①②及A1A、AC是平面A1ACC1内的两条相交直线,
得BD⊥平面A1ACC1.
法二:由A1A⊥平面ABC,A1A平面A1ACC1,
∴平面A1ACC1⊥平面ABC,又平面A1ACC1∩平面ABC=AC,
得BD⊥平面A1ACC1.
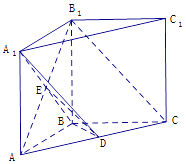
(2)解:由AB=1,得BC=BB1=1,
由(1)知DA= ![]() AC,又ACDA=1,得AC2=2,
AC,又ACDA=1,得AC2=2,
∵AC2=2=AB2+BC2,∴AB⊥BC,
如图以B为原点,建立空间直角坐标系B﹣xyz,如图示,
则A1(1,0,1),B1(0,0,1),D( ![]() ),
),
得 ![]() =(1,0,0),
=(1,0,0), ![]() =(
=( ![]() ),
),
设 ![]() =(x,y,z)是平面A1B1D的一个法向量,
=(x,y,z)是平面A1B1D的一个法向量,
则 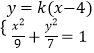 ,令z=1,得
,令z=1,得 ![]() =(0,2,1),
=(0,2,1),
设 ![]() =(a,b,c)为平面A1BD的一个法向量,则
=(a,b,c)为平面A1BD的一个法向量,则 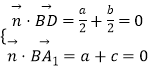 ,
,
令c=1,得 ![]() =(﹣1,1,1),
=(﹣1,1,1),
依题意知二面角B﹣A1D﹣B1为锐二面角,设其大小为θ,
则cosθ=|cos< ![]() >|=
>|= ![]() =
= ![]() =
= ![]() ,
,
即二面角B﹣A1D﹣B1的余弦值为 ![]() .
.
其它解法请参照给分.

【解析】(Ⅰ)法一:连结ED,推导出B1C∥ED,BD⊥AC,A1A⊥BD,由此能证明BD⊥平面A1ACC1 . 法二:连结ED,推导出A1A⊥平面ABC,由平面A1ACC1⊥平面ABC,能证明BD⊥平面A1ACC1 . (Ⅱ)以B为原点,建立空间直角坐标系B﹣xyz,利用向量法能求出二面角B﹣A1D﹣B1的余弦值.
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】如图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的”更相减损术“.执行该程序框图,若输入a,b,i的值分别为6,8,0时,则输出的i=( ) 
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若命题p:?x0∈R,x02﹣x0+1<0,则¬p:?x?R,x2﹣x+1≥0
B.已知相关变量(x,y)满足回归方程 ![]() =2﹣4x,若变量x增加一个单位,则y平均增加4个单位
=2﹣4x,若变量x增加一个单位,则y平均增加4个单位
C.命题“若圆C:(x﹣m+1)2+(y﹣m)2=1与两坐标轴都有公共点,则实数m∈[0,1]为真命题
D.已知随机变量X~N(2,σ2),若P(X<a)=0.32,则P(X>4﹣a)=0.68
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有人持金出五关,前关二而税一,次关三而税一,次关四而税一,次关五而税一,次关六而税一,并五关所税,适重一斤,问本持金几何”其意思为“今有人持金出五关,第1关收税金 ![]() ,第2关收税金为剩余金的
,第2关收税金为剩余金的 ![]() ,第3关收税金为剩余金的
,第3关收税金为剩余金的 ![]() ,第4关收税金为剩余金的
,第4关收税金为剩余金的 ![]() ,第5关收税金为剩余金的
,第5关收税金为剩余金的 ![]() ,5关所收税金之和,恰好重1斤,问原来持金多少?”若将题中“5关所收税金之和,恰好重1斤,问原来持金多少?”改成假设这个原来持金为x,按此规律通过第8关,则第8关需收税金为x.
,5关所收税金之和,恰好重1斤,问原来持金多少?”若将题中“5关所收税金之和,恰好重1斤,问原来持金多少?”改成假设这个原来持金为x,按此规律通过第8关,则第8关需收税金为x.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|2x﹣a|+a.
(1)当a=3时,求不等式f(x)≤6的解集;
(2)设函数g(x)=|2x﹣3|,x∈R,f(x)+g(x)≥5,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[不等式选讲]
设函数f(x)=a(x﹣1).
(Ⅰ)当a=1时,解不等式|f(x)|+|f(﹣x)|≥3x;
(Ⅱ)设|a|≤1,当|x|≤1时,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+x2﹣x,其中a∈R.
(Ⅰ)若a>0,讨论f(x)的单调性;
(Ⅱ)当x≥1时,f(x)≥0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的短轴长为2
的短轴长为2 ![]() ,离心率e=
,离心率e= ![]() ,
,
(1)求椭圆C的标准方程:
(2)若F1、F2分别是椭圆C的左、右焦点,过F2的直线l与椭圆C交于不同的两点A、B,求△F1AB的内切圆半径的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数 ![]() 的图像向左平移
的图像向左平移 ![]() 个单位,再向上平移1个单位,得到g(x)的图像.若g(x1)g(x2)=9,且x1 , x2∈[﹣2π,2π],则2x1﹣x2的最大值为( )
个单位,再向上平移1个单位,得到g(x)的图像.若g(x1)g(x2)=9,且x1 , x2∈[﹣2π,2π],则2x1﹣x2的最大值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com