
分析 (I)可假设存在实数a,b,使得y=f(x)的定义域和值域都是[a,b],由此出发探究a,b的可能取值,可分三类:a,b∈(0,$\frac{1}{2}$)时,a,b∈($\frac{1}{2}$,+∞)时,a∈(0,$\frac{1}{2}$),b∈($\frac{1}{2}$,+∞),分别建立方程,寻求a,b的可能取值,若能求出这样的实数,则说明存在,否则说明不存在;
(II)由题意,由函数y=f (x)的定义域为[a,b],值域为[ma,mb](m≠0)可判断出m>0及a>0,结合(I)的结论知只能a,b∈($\frac{1}{2}$,+∞),由函数在此区间内是增函数,建立方程,即可得到实数m所满足的不等式,解出实数m的取值范围.
解答 解:(I)不存在实数a,b满足条件.
假设存在实数a,b,使得y=f(x)的定义域和值域都是[a,b],
而y≥0,x≠0,所以应有a>0,
又f(x)=$\left\{\begin{array}{l}{2-\frac{1}{x},x≥\frac{1}{2}}\\{\frac{1}{x}-2,0<x<\frac{1}{2}}\end{array}\right.$
(1)当a,b∈(0,$\frac{1}{2}$)时,f(x)=$\frac{1}{x}$-2在(0,$\frac{1}{2}$)上为减函数,
故有 $\left\{\begin{array}{l}{f(a)=b}\\{f(b)=a}\end{array}\right.$,即 $\left\{\begin{array}{l}{\frac{1}{a}-2=b}\\{\frac{1}{b}-2=a}\end{array}\right.$,由此可得a=b,此时实数a,b的值不存在.
(2)当a,b∈[$\frac{1}{2}$,+∞)时,f(x)=2-$\frac{1}{x}$在∈($\frac{1}{2}$,+∞)上为增函数,
故有 $\left\{\begin{array}{l}{f(a)=a}\\{f(b)=b}\end{array}\right.$,即$\left\{\begin{array}{l}{2-\frac{1}{a}=a}\\{2-\frac{1}{b}=b}\end{array}\right.$由此可得a,b是方程x2-2x+1=0的根,但方程有两个相等实根,所以此时不成立.
(3)当a∈(0,$\frac{1}{2}$),b∈($\frac{1}{2}$,+∞)时,显然$\frac{1}{2}$∈[a,b],而f($\frac{1}{2}$)=0∈[a,b]不可能,
此时a,b也不存在;
综上可知,适合条件的实数a,b不存在.
(II)若存在实数a,b使函数y=f(x)的定义域为[a,b],值域为[ma,mb](m≠0).
由mb>ma,b>a得m>0,而ma>0,所以a>0
由(I)知a,b∈(0,$\frac{1}{2}$)或a∈(0,$\frac{1}{2}$),b∈($\frac{1}{2}$,+∞)时,适合条件的实数a,b不存在,
故只能是a,b∈($\frac{1}{2}$,+∞)
∵f(x)=2-$\frac{1}{x}$在∈($\frac{1}{2}$,+∞)上为增函数,
∴$\left\{\begin{array}{l}{f(a)=ma}\\{f(b)=mb}\end{array}\right.$,即$\left\{\begin{array}{l}{2-\frac{1}{a}=ma}\\{2-\frac{1}{b}=mb}\end{array}\right.$∴a,b是方程mx2-2x+1=0的两个不等实根,
且二实根均大于$\frac{1}{2}$,
∴$\left\{\begin{array}{l}{△=4-4m>0}\\{\frac{1}{4}m-1+1>0}\\{\frac{1}{m}>\frac{1}{2}}\end{array}\right.$,解之得0<m<1,
故实数m的取值范围是(0,1).
点评 本题的考点是函数与方程的综合应用,考察了绝对值函数,函数的定义域、值域构造方程的思想,二次方程根与系数的关系等,解题的关键是理解题意,将问题正确转化,进行分类讨论探究,本题考察了分类讨论的思想,方程的思想,考察了推理判断能力,是一道综合性较强的题,思维难度大,解题时要严谨,本题易因为考虑不完善出错.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-3<x<0} | B. | {x|-1<x<0} | C. | {x|0<x<1} | D. | {x|0<x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
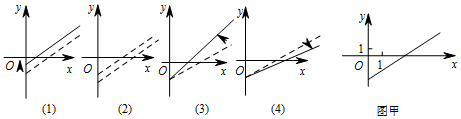
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com