[题目]若函数f(x)的定义域为[2a﹣1.a+1].值域为[a+3.4a].则a的取值范围为．题目和参考答案——青夏教育精英家教网—

【题目】若函数f（x）的定义域为[2a﹣1，a+1]，值域为[a+3，4a]，则a的取值范围为．

【答案】1＜a＜2
【解析】∵函数f（x）的定义域为[2a﹣1，a+1]，值域为[a+3，4a]，

∴2a﹣1＜a+1，a+3＜4a，

解得，1＜a＜2．

所以答案是：1＜a＜2．

【考点精析】根据题目的已知条件，利用函数的定义域及其求法和函数的值域的相关知识可以得到问题的答案，需要掌握求函数的定义域时，一般遵循以下原则：①是整式时，定义域是全体实数;②是分式函数时，定义域是使分母不为零的一切实数;③是偶次根式时，定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1,零（负）指数幂的底数不能为零；求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数f（x）= ，
（1）判断函数在区间[1，+∞）上的单调性，并用定义证明你的结论；
（2）求该函数在区间[1，4]上的最大值与最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是直角梯形，AD⊥AB，AB∥DC，PA⊥底面ABCD，点E为棱PC的中点．AD=DC=AP=2AB=2．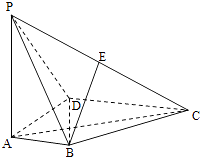

（1）证明：BE⊥平面PDC；
（2）若F为棱PC上一点，满足BF⊥AC，求二面角F﹣AD﹣C的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】连江一中第49届田径运动会提出了“我运动、我阳光、我健康、我快乐”的口号，某同学要设计一张如图所示的竖向张贴的长方形海报进行宣传，要求版心面积为162dm2（版心是指图中的长方形阴影部分，dm为长度单位分米），上、下两边各空2dm，左、右两边各空1dm．

（1）若设版心的高为xdm，求海报四周空白面积关于x的函数S（x）的解析式；
（2）要使海报四周空白面积最小，版心的高和宽该如何设计？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知数列{an}的前n项和为Sn ，对任意的n∈N* ，点（n，Sn）恒在函数y= x的图象上．
（1）求数列{an}的通项公式；
（2）记Tn= ，若对于一切的正整数n，总有Tn≤m成立，求实数m的取值范围；
（3）设Kn为数列{bn}的前n项和，其中bn=2an ，问是否存在正整数n，t，使成立？若存在，求出正整数n，t；若不存在，请说明理由．