(10分) 已知等比数列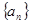
中，
，求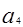
及其前5项的和
.
黎明文化寒假作业系列答案
寒假天地重庆出版社系列答案科目：高中数学 来源：2012届浙江省台州中学高三上学期第一次统练理科数学 题型：解答题
（本题满分10分）已知曲线
上的动点
满足到点
的距离比到直线 
的距离小
．
（1）求曲线的方程；
（2）动点
在直线 
上，过点作曲线的切线
，切点分别为
、
．
（ⅰ）求证：直线
恒过一定点，并求出该定点的坐标；
（ⅱ）在直线上是否存在一点，使得
为等边三角形（
点也在直线上）？若存在，求出点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源：2011-2012学年浙江省高三上学期第一次统练理科数学 题型：解答题
（本题满分10分）已知曲线
上的动点
满足到点
的距离比到直线 
的距离小
．
（1）求曲线的方程；
（2）动点
在直线 
上，过点作曲线的切线
，切点分别为
、
．
（ⅰ）求证：直线
恒过一定点，并求出该定点的坐标；
（ⅱ）在直线上是否存在一点，使得
为等边三角形（
点也在直线上）？若存在，求出点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
（共14分，6分+8分）
某企业去年的纯利润为500万元，因设备老化等原因，企业的生产能力将逐年下降。若不进行技术改造，预测今年起每年比上一年的纯利润减少20万元。今年初该企业一次性投入资金600万元进行技术改造，预测在未扣除技术改造资金的情况下，第n年（今年为第一年）的利润为500（1+）万元（n为正整数）。设从今年起的前n年,若该企业不进行技术改造的累计纯利润为An万元,进行技术改造后的累计纯利润为Bn万元（需扣除技术改造资金）
（1）、求An、Bn的表达式;（2）、依上述预测，从今年起该企业至少经过多少年，进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润？
23（共10分，每个空格2分）
课本在介绍“i2=-1的几何意义”中讲到：将复平面上的向量乘以i就是沿逆时针方向旋转900，那么乘以-i就是沿顺时针方向旋转900。做以下填空：
已知复平面上的向量
分别对应复数3-i、-2+i，则向量
对应的复数为 ；那么，以线段MN为一边作两个正方形MNQP和MNQ,P,,则点P、Q对应的复数分别为 、 ；点P，、Q，对应的复数分别为 、 。
查看答案和解析>>
科目：高中数学 来源： 题型：
（共14分，6分+8分）
某企业去年的纯利润为500万元，因设备老化等原因，企业的生产能力将逐年下降。若不进行技术改造，预测今年起每年比上一年的纯利润减少20万元。今年初该企业一次性投入资金600万元进行技术改造，预测在未扣除技术改造资金的情况下，第n年（今年为第一年）的利润为500（1+）万元（n为正整数）。设从今年起的前n年,若该企业不进行技术改造的累计纯利润为An万元,进行技术改造后的累计纯利润为Bn万元（需扣除技术改造资金）
（1）、求An、Bn的表达式;（2）、依上述预测，从今年起该企业至少经过多少年，进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润？
23（共10分，每个空格2分）
课本在介绍“i2=-1的几何意义”中讲到：将复平面上的向量乘以i就是沿逆时针方向旋转900，那么乘以-i就是沿顺时针方向旋转900。做以下填空：
已知复平面上的向量
分别对应复数3-i、-2+i，则向量
对应的复数为 ；那么，以线段MN为一边作两个正方形MNQP和MNQ,P,,则点P、Q对应的复数分别为 、 ；点P，、Q，对应的复数分别为 、 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
，
，进而得到通项公式，从而得到求和。
， ┄┄┄┄┄┄┄┄┄┄┄1分
┄┄┄┄┄┄┄┄┄┄┄ 3分
①
┄┄┄┄┄┄┄┄┄┄┄┄┄ 4分
， ┄┄┄┄┄┄┄┄┄┄ 7分
， ┄┄┄┄┄┄┄┄┄┄┄ 9分
┄┄┄┄┄┄ 10分
