
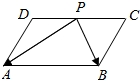
 如图,在平行四边形ABCD中,AB=6,AD=4.点P是DC边的中点,则$\overrightarrow{PA}•\overrightarrow{PB}$的值为7.
如图,在平行四边形ABCD中,AB=6,AD=4.点P是DC边的中点,则$\overrightarrow{PA}•\overrightarrow{PB}$的值为7. 分析 把$\overrightarrow{PA}•\overrightarrow{PB}$中的两个向量用基底<$\overrightarrow{AB},\overrightarrow{AD}$>表示,展开后得答案.
解答 解:∵AB=6,AD=4,
∴$\overrightarrow{PA}•\overrightarrow{PB}$=$(\overrightarrow{PD}+\overrightarrow{DA})•(\overrightarrow{PC}+\overrightarrow{CB})$
=$(-\frac{1}{2}\overrightarrow{AB}-\overrightarrow{AD})•(\frac{1}{2}\overrightarrow{AB}-\overrightarrow{AD})$
=$-\frac{1}{4}|\overrightarrow{AB}{|}^{2}+|\overrightarrow{AD}{|}^{2}$=$-\frac{1}{4}×36+16=7$.
故答案为:7.
点评 本题考查平面向量的数量积运算,关键是把要求数量积的向量用基底<$\overrightarrow{AB},\overrightarrow{AD}$>表示,是中档题.


科目:高中数学 来源: 题型:解答题
 如图,∠AOP=$\frac{π}{3}$,Q点与P点关于y轴对称,P,Q都为角的终边与单位圆的交点,求:
如图,∠AOP=$\frac{π}{3}$,Q点与P点关于y轴对称,P,Q都为角的终边与单位圆的交点,求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com