
分析 (Ⅰ)运用椭圆的离心率公式和a,b,c的关系,计算即可得到b,进而得到椭圆C的方程;
(Ⅱ)求得椭圆E的方程,(i)设P(x0,y0),|$\frac{OQ}{OP}$|=λ,求得Q的坐标,分别代入椭圆C,E的方程,化简整理,即可得到所求值;
(ii)设A(x1,y1),B(x2,y2),将直线y=kx+m代入椭圆E的方程,运用韦达定理,三角形的面积公式,将直线y=kx+m代入椭圆C的方程,由判别式大于0,可得t的范围,结合二次函数的最值,又△ABQ的面积为3S,即可得到所求的最大值.
解答 解:(Ⅰ)由题意可知,PF1+PF2=2a=3+1=4,可得a=2,
又$\frac{c}{a}$=$\frac{1}{2}$,a2-c2=b2,
可得c=1,b=$\sqrt{3}$,即有椭圆C的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(Ⅱ)由(Ⅰ)知椭圆E的方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1,
(i)设P(x0,y0),|$\frac{OQ}{OP}$|=λ,由题意可知,
Q(-λx0,-λy0),由于$\frac{{{x}_{0}}^{2}}{4}$+$\frac{{{y}_{0}}^{2}}{3}$=1,
又$\frac{(-λ{x}_{0})^{2}}{16}$+$\frac{(-λ{y}_{0})^{2}}{12}$=1,即$\frac{{λ}^{2}}{4}$($\frac{{{x}_{0}}^{2}}{4}$+$\frac{{{y}_{0}}^{2}}{3}$)=1,
所以λ=2,即|$\frac{OQ}{OP}$|=2;
(ii)设A(x1,y1),B(x2,y2),将直线y=kx+m代入椭圆E的方程,可得
(3+4k2)x2+8kmx+4m2-48=0,由△>0,可得m2<12+16k2,①
则有x1+x2=-$\frac{8km}{3+4{k}^{2}}$,x1x2=$\frac{4{m}^{2}-48}{3+4{k}^{2}}$,
所以|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{4\sqrt{3}•\sqrt{16{k}^{2}+12-{m}^{2}}}{3+4{k}^{2}}$,
由直线y=kx+m与y轴交于(0,m),
则△AOB的面积为S=$\frac{1}{2}$|m|•|x1-x2|=$\frac{1}{2}$|m|•$\frac{4\sqrt{3}•\sqrt{16{k}^{2}+12-{m}^{2}}}{3+4{k}^{2}}$
=2$\sqrt{3}$$\sqrt{(4-\frac{{m}^{2}}{3+4{k}^{2}})•\frac{{m}^{2}}{3+4{k}^{2}}}$,设$\frac{{m}^{2}}{3+4{k}^{2}}$=t,则S=2$\sqrt{3}$$\sqrt{t(4-t)}$,
将直线y=kx+m代入椭圆C的方程,可得(3+4k2)x2+8kmx+4m2-12=0,
由△≥0可得m2≤3+4k2,②
由①②可得0<t≤1,则S=2$\sqrt{3}$$\sqrt{4-(t-2)^{2}}$在(0,1]递增,即有t=1取得最大值,
即有S≤6,即m2=3+4k2,取得最大值6,
由(i)知,△ABQ的面积为3S,
即△ABQ面积的最大值为18.
点评 本题考查椭圆的方程和性质,主要考查直线方程和椭圆方程联立,运用韦达定理,同时考查三角形的面积公式和二次函数的最值,属于难题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |PP1|=|AA1|+|BB1| | B. | |PP1|=$\frac{1}{2}$|AB| | C. | |PP1|>$\frac{1}{2}$|AB| | D. | |PP1|$<\frac{1}{2}$|AB| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
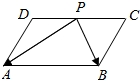 如图,在平行四边形ABCD中,AB=6,AD=4.点P是DC边的中点,则$\overrightarrow{PA}•\overrightarrow{PB}$的值为7.
如图,在平行四边形ABCD中,AB=6,AD=4.点P是DC边的中点,则$\overrightarrow{PA}•\overrightarrow{PB}$的值为7.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
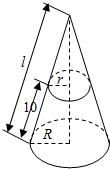 把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:2,母线长10cm.圆台侧面展开是一个$\frac{1}{4}$圆环,求:
把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:2,母线长10cm.圆台侧面展开是一个$\frac{1}{4}$圆环,求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 7 | C. | 9 | D. | 7或8或9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com