
| 1 |
| 4 |
| 3 |
| 4 |
| 7 |
| 16 |
| C | 1 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 7 |
| 16 |
| C | 1 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 7 |
| 16 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
| 2 |
| 3 |
| 3 |
| 8 |
| 7 |
| 16 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
| 3 |
| C | 1 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 48 |
| ξ | 0 | 1 | 2 | 3 | ||||||||
|
|
|
|
| 3 |
| 8 |
| 7 |
| 16 |
| 1 |
| 6 |
| 1 |
| 48 |
| 5 |
| 6 |
| 5 |
| 6 |


科目:高中数学 来源: 题型:
(本小题满分12分)学校要用三辆校车从南校区把教职工接到校本部,已知从南校区到校本部有两条公路,校车走公路①堵车的概率为![]() ,不堵车的概率为
,不堵车的概率为![]() ;校车走公路②堵车的概率为
;校车走公路②堵车的概率为![]() ,不堵车的概率为
,不堵车的概率为![]() .若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.(Ⅰ)若三辆校车中恰有一辆校车被堵的概率为
.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.(Ⅰ)若三辆校车中恰有一辆校车被堵的概率为![]() ,求走公路②堵车的概率;(Ⅱ)在(1)的条件下,求三辆校车中被堵车辆的辆数
,求走公路②堵车的概率;(Ⅱ)在(1)的条件下,求三辆校车中被堵车辆的辆数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省南昌市新建二中高三(上)9月月考数学试卷(理科)(解析版) 题型:解答题
 ,不堵车的概率为
,不堵车的概率为 ;校车走公路②堵车的概率为,不堵车的概率为1-p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
;校车走公路②堵车的概率为,不堵车的概率为1-p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.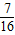 ,求走公路②堵车的概率;
,求走公路②堵车的概率;查看答案和解析>>
科目:高中数学 来源:2012年四川省成都市石室中学高考数学三模试卷(理科)(解析版) 题型:解答题
 ,不堵车的概率为
,不堵车的概率为 ;校车走公路②堵车的概率为,不堵车的概率为1-p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
;校车走公路②堵车的概率为,不堵车的概率为1-p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.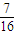 ,求走公路②堵车的概率;
,求走公路②堵车的概率;查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省内江市威远中学高三选填题强化训练11(理科)(解析版) 题型:解答题
 ,不堵车的概率为
,不堵车的概率为 ;校车走公路②堵车的概率为,不堵车的概率为1-p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
;校车走公路②堵车的概率为,不堵车的概率为1-p.若甲、乙两辆校车走公路①,丙校车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响. ,求走公路②堵车的概率;
,求走公路②堵车的概率;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com