
对n∈N?不等式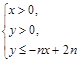 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列(x1,y1),(x2,y2),?,(xn,yn),
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列(x1,y1),(x2,y2),?,(xn,yn),
求xn,yn;
(2)数列{an}满足a1=x1,且n≥2时an=yn2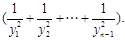 证明:当n≥2时,
证明:当n≥2时,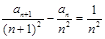 ;
;
(3)在(2)的条件下,试比较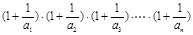 与4的大小关系.
与4的大小关系.
科目:高中数学 来源: 题型:解答题
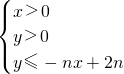 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).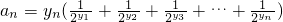 ,求数列{an}的前n项和Sn;
,求数列{an}的前n项和Sn;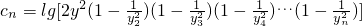 ,且数列{cn}的前n项和Tn,求T99.
,且数列{cn}的前n项和Tn,求T99.查看答案和解析>>
科目:高中数学 来源: 题型:
 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成一列点:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成一列点:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).(Ⅰ)求xn、yn;
(Ⅱ)若an=3n+λ·(-xn)n-1·![]() (λ为非零常数),问是否存在整数λ,使得对任意n∈N*,都有an+1>an.
(λ为非零常数),问是否存在整数λ,使得对任意n∈N*,都有an+1>an.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省泰安市新泰一中高二(上)期中数学试卷(理科)(解析版) 题型:解答题
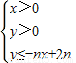 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn). ,求数列{an}的前n项和Sn;
,求数列{an}的前n项和Sn;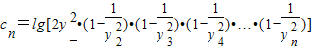 ,且数列{cn}的前n项和Tn,求T99.
,且数列{cn}的前n项和Tn,求T99.查看答案和解析>>
科目:高中数学 来源:2007年湖北省黄冈中学、华师一附中、鄂南高中、黄石二中、孝感高中、荆州中学、襄樊四中、襄樊五中高三第二次联考数学试卷(文科)(解析版) 题型:解答题
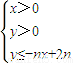 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成一列点:(x1,y1),(x2,y2),(x3,y4),…,(xn,yn)
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成一列点:(x1,y1),(x2,y2),(x3,y4),…,(xn,yn)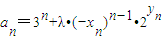 (λ为非零常数),问是否存在整数λ,使得对任意n∈N*,都有an+1>an.
(λ为非零常数),问是否存在整数λ,使得对任意n∈N*,都有an+1>an.查看答案和解析>>
科目:高中数学 来源:2010年湖南省澧县一中、岳阳一中高三第三次联考数学试卷(文科)(解析版) 题型:解答题
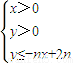 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn). ,求数列{an}的前n项和Sn;
,求数列{an}的前n项和Sn; ,且数列{cn}的前n项和Tn,求T99.
,且数列{cn}的前n项和Tn,求T99.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com