
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,以
,以![]() 为圆心过椭圆左顶点
为圆心过椭圆左顶点![]() 的圆与直线
的圆与直线![]() 相切于
相切于![]() ,且满足
,且满足![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,问
,问![]() 内切圆面积是否有最大值?若有,求出最大值;若没有,说明理由.
内切圆面积是否有最大值?若有,求出最大值;若没有,说明理由.
【答案】(1)![]() ;(2)有,最大值
;(2)有,最大值![]()
【解析】
(1)由已知可得![]() 到直线
到直线![]() 的距离等于
的距离等于![]() ,结合
,结合![]() ,建立
,建立![]() 方程组,求解即可得出椭圆
方程组,求解即可得出椭圆![]() 的标准方程;
的标准方程;
(2)即求![]() 内切圆的半径
内切圆的半径![]() 是否有最大值,因为
是否有最大值,因为![]() 周长为
周长为![]() ,转化为
,转化为![]() 的面积是否有最大值,设
的面积是否有最大值,设![]() ,则
,则![]() ,再设出直线
,再设出直线![]() 的方程为
的方程为![]() ,与椭圆方程联立,得出
,与椭圆方程联立,得出![]() 关系,
关系,![]() 表示为
表示为![]() 的函数,根据其特征求出范围,即可得出结论.
的函数,根据其特征求出范围,即可得出结论.
(1)由已知椭圆![]() 方程为
方程为![]() ,
,
设椭圆右焦点![]() ,由
,由![]() 到直线
到直线![]() 的距离等于
的距离等于![]() ,
,
得![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
又![]() ,求得
,求得![]() ,
,![]() .
.
椭圆![]() 方程为
方程为![]() ,
,
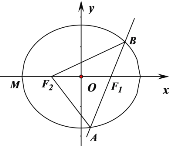
(2)设![]() ,
,![]() ,设
,设![]() 的内切圆半径为
的内切圆半径为![]() ,
,
![]() 的周长为
的周长为![]() ,
,
所以![]() ,
,
根据题意,直线![]() 的斜率不为零,可设直线
的斜率不为零,可设直线![]() 的方程为
的方程为![]() ,
,
由 ,得
,得![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以![]() ,
,
令![]() ,则
,则![]() ,所以
,所以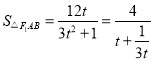 ,
,
令![]() ,则当
,则当![]() 时,
时,![]() ,
,
![]() 单调递增,所以
单调递增,所以![]() ,
,![]() ,
,
即当![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() 时,
时,
![]() 的最大值为3,此时内切圆半径最大
的最大值为3,此时内切圆半径最大![]() ,
,
![]() 内切圆面积有最大值
内切圆面积有最大值![]() .
.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() 的前
的前![]() 项中的最大项为
项中的最大项为![]() ,最小项为
,最小项为![]() ,设
,设![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() :
:![]() 与曲线
与曲线![]() :
:![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(Ⅰ)求曲线![]() 的方程.
的方程.
(Ⅱ)设过曲线![]() 焦点
焦点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,记直线
两点,记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .求证:
.求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() ,不与
,不与![]() 轴垂直的直线
轴垂直的直线![]() 与双曲线右支交于点
与双曲线右支交于点![]() ,
,![]() ,(
,(![]() 在
在![]() 轴上方,
轴上方,![]() 在
在![]() 轴下方),与双曲线渐近线交于点
轴下方),与双曲线渐近线交于点![]() ,
,![]() (
(![]() 在
在![]() 轴上方),
轴上方),![]() 为坐标原点,下列选项中正确的为( )
为坐标原点,下列选项中正确的为( )
A.![]() 恒成立
恒成立
B.若![]() ,则
,则![]()
C.![]() 面积的最小值为1
面积的最小值为1
D.对每一个确定的![]() ,若
,若![]() ,则
,则![]() 的面积为定值
的面积为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 为抛物线
为抛物线![]() 上一点,斜率分别为
上一点,斜率分别为![]() ,
,![]()
![]() 的直线PA,PB分别交抛物线于点A,B(不与点P重合).
的直线PA,PB分别交抛物线于点A,B(不与点P重合).

(1)证明:直线AB的斜率为定值;
(2)若△ABP的内切圆半径为![]() .
.
(i)求△ABP的周长(用k表示);
(ii)求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国唐代天文学家、数学家张逐曾以“李白喝酒”为题编写了如下一道题:“李白街上走,提壶去买酒,遇店加一倍,见花喝一斗(计量单位),三遇店和花,喝光壶中酒.”问最后一次遇花时有酒________斗,原有酒________斗.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com