
【题目】已知在四面体ABCD中,E,F分别是AC,BD的中点,若AB=2,CD=4,EF⊥AB,则EF与CD所成的角的度数为( )
A.90°
B.45°
C.60°
D.30°
【答案】D
【解析】解:设G为AD的中点,连接GF,GE, 
则GF,GE分别为△ABD,△ACD的中线.
由此可得,GF∥AB且GF= ![]() AB=1,
AB=1,
GE∥CD,且GE= ![]() CD=2,
CD=2,
∴∠FEG或其补角即为EF与CD所成角.
又∵EF⊥AB,GF∥AB,∴EF⊥GF
因此,Rt△EFG中,GF=1,GE=2,
由正弦的定义,得sin∠GEF= ![]() =
= ![]() ,可得∠GEF=30°.
,可得∠GEF=30°.
∴EF与CD所成的角的度数为30°
故选:D
【考点精析】通过灵活运用异面直线及其所成的角,掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系即可以解答此题.


科目:高中数学 来源: 题型:
【题目】河道上有一座圆拱桥,在正常水位时,拱圈最高点距水面9m,拱圈内水面宽22m.一条船在水面以上部分高6.5m,船顶部宽4m,故通行无阻.近日水位暴涨了2.7m,为此,必须加重舰载,降低船身,才能通过桥洞.试问船身至少应该降低多少?(精确到0.01,参考数据: ![]() )
) 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是公差为1的等差数列,a1 , a5 , a25成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=3 ![]() +an , 求数列{bn}的前n项和Tn .
+an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人进行乒乓球决赛,比赛采取七局四胜制.现在的情形是甲胜3局,乙胜2局.若两人胜每局的概率相同,则甲获得冠军的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() :
: ![]() (
(![]() )上,设
)上,设![]() ,
, ![]() ,
, ![]() 分别为左顶点、上顶点、下顶点,且下顶点
分别为左顶点、上顶点、下顶点,且下顶点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设点![]() ,
, ![]() (
(![]() )为椭圆
)为椭圆![]() 上两点,且满足
上两点,且满足![]() ,求证:
,求证: ![]() 的面积为定值,并求出该定值.
的面积为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具厂有方木料![]() ,五合板
,五合板![]() ,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料
,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料![]() 、五合板
、五合板![]() ;生产每个书橱需要方木枓
;生产每个书橱需要方木枓![]() 、五合板
、五合板![]() .出售一张书桌可获利润
.出售一张书桌可获利润![]() 元,出售一个书橱可获利润
元,出售一个书橱可获利润![]() 元,怎样安排生产可使所得利润最大?最大利润为多少?
元,怎样安排生产可使所得利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为缓解高三学生的高考压力,经常举行一些心理素质综合能力训练活动,经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试,并将其成绩分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个等级,统计数据如图所示(视频率为概率),根据图中抽样调查的数据,回答下列问题:
五个等级,统计数据如图所示(视频率为概率),根据图中抽样调查的数据,回答下列问题:
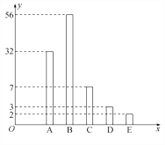
(1)试估算该校高三年级学生获得成绩为![]() 的人数;
的人数;
(2)若等级![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分别对应100分、90分、80分、70分、60分,学校要求当学生获得的等级成绩的平均分大于90分时,高三学生的考前心理稳定,整体过关,请问该校高三年级目前学生的考前心理稳定情况是否整体过关?
分别对应100分、90分、80分、70分、60分,学校要求当学生获得的等级成绩的平均分大于90分时,高三学生的考前心理稳定,整体过关,请问该校高三年级目前学生的考前心理稳定情况是否整体过关?
(3)以每个学生的心理都培养成为健康状态为目标,学校决定对成绩等级为![]() 的16名学生(其中男生4人,女生12人)进行特殊的一对一帮扶培训,从按分层抽样抽取的4人中任意抽取2名,求恰好抽到1名男生的概率..
的16名学生(其中男生4人,女生12人)进行特殊的一对一帮扶培训,从按分层抽样抽取的4人中任意抽取2名,求恰好抽到1名男生的概率..
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com