练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知椭圆C1：＋y2＝1，椭圆C2以C1的长轴为短轴，且与C1有相同的离心率．

    (1)求椭圆C2的方程；

    (2)设O为坐标原点，点A，B分别在椭圆C1和C2上，＝2，求直线AB的方程．

     

    （1）＝1（2）y＝x或y＝－x

    【解析】(1)由已知可设椭圆C2的方程为＝1(a>2)，

    其离心率为，故＝，解得a＝4.故椭圆C2的方程为＝1.

    (2)A，B两点的坐标分别记为(xA，yA)，(xB，yB)，

    由＝2及(1)知，O，A，B三点共线且点A，B不在y轴上，因此可设直线AB的方程为y＝kx.

    将y＝kx代入＋y2＝1中，得(1＋4k2)x2＝4，所以.

    将y＝kx代入＝1中，得(4＋k2)x2＝16，所以.

    又由＝2，得，

    ∴，解得k＝±1.

    故直线AB的方程为y＝x或y＝－x.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练选修4-4练习卷（解析版） 题型：填空题

    已知曲线C的极坐标方程为ρ＝2cos θ，以极点为原点，极轴为x轴的正半轴建立直角坐标系，则曲线C的参数方程为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-7-2练习卷（解析版） 题型：选择题

    如图，将一个各面都涂了油漆的正方体，切割为125个同样大小的小正方体，经过搅拌后，从中随机取一个小正方体，记它的油漆面数为X，则X的均值E(X)等于(　　)．

    A. B. C. D.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-6-3练习卷（解析版） 题型：解答题

    已知A，B，C是椭圆W：＋y2＝1上的三个点，O是坐标原点．

    (1)当点B是W的右顶点，且四边形OABC为菱形时，求此菱形的面积；

    (2)当点B不是W的顶点时，判断四边形OABC是否可能为菱形，并说明理由．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-6-3练习卷（解析版） 题型：选择题

    从椭圆＝1(a>b>0)上一点P向x轴作垂线，垂足恰为左焦点F1，A是椭圆与x轴正半轴的交点，B是椭圆与y轴正半轴的交点，且AB∥OP(O是坐标原点)，则该椭圆的离心率是(　　)．

    A. B. C. D.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-6-2练习卷（解析版） 题型：选择题

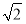    O为坐标原点，F为抛物线C：y2＝4x的焦点，P为C上一点，若|PF|＝4，则△POF的面积为(　　)．

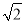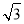    A．2 B．2 C．2 D．4

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-6-1练习卷（解析版） 题型：填空题

    设圆x2＋y2＝2的切线l与x轴的正半轴、y轴的正半轴分别交于点A，B，当|AB|取最小值时，切线l的方程为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-5-3练习卷（解析版） 题型：选择题

    如图所示，在空间直角坐标系中有直三棱柱ABC－A1B1C1，CA＝CC1＝2CB，则直线BC1与直线AB1夹角的余弦值为(　　)．

    A. B. C. D.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮专题复习知能提升演练1-4-1练习卷（解析版） 题型：选择题

    公比为2的等比数列{an}的各项都是正数，且a3a11＝16，则log2a10＝(　　)．

    A．4 B．5

    C．6 D．7

     

    查看答案和解析>>

    同步练习册答案