
已知椭圆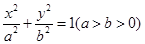 的左、右焦点分别是
的左、右焦点分别是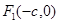 、
、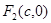 ,离心率为
,离心率为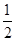 ,椭圆上的动点
,椭圆上的动点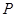 到直线
到直线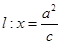 的最小距离为2,延长
的最小距离为2,延长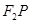 至
至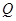 使得
使得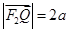 ,线段
,线段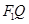 上存在异于
上存在异于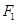 的点
的点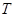 满足
满足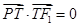 .
.
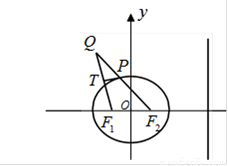
(1) 求椭圆的方程;
(2)
求点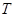 的轨迹
的轨迹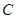 的方程;
的方程;
(3)
求证:过直线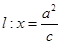 上任意一点必可以作两条直线
上任意一点必可以作两条直线
与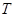 的轨迹
的轨迹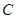 相切,并且过两切点的直线经过定点.
相切,并且过两切点的直线经过定点.
(1)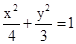 ;(2)
;(2)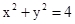 ;(3)直线经过定点(1,0).
;(3)直线经过定点(1,0).
【解析】本试题主要考查了圆与直线,以及椭圆的方程,直线与椭圆的位置关系的综合运用。
解:(1)依题意得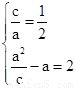 , ………………………………………………2分
, ………………………………………………2分
解得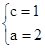 ,∴
,∴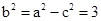 ……………………………………………………………3分
……………………………………………………………3分
椭圆的方程为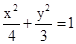 …………………………………………………………………4分
…………………………………………………………………4分
(2)解法1:设点T的坐标为(x,y).
当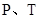 重合时,点
重合时,点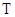 坐标为
坐标为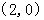 和点
和点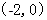 ,
…………………………………5分
,
…………………………………5分
当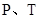 不重合时,由
不重合时,由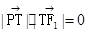 ,得
,得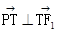 . ……………………………6分
. ……………………………6分
由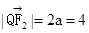 及椭圆的定义,
及椭圆的定义,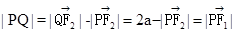 , …………7分
, …………7分
所以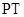 为线段
为线段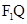 的垂直平分线,T为线段
的垂直平分线,T为线段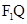 的中点
的中点
在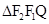 中,
中,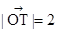 , …………………………………………8分
, …………………………………………8分
所以有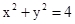 .
.
综上所述,点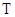 的轨迹C的方程是
的轨迹C的方程是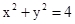 . …………………………………9分
. …………………………………9分
(3)
直线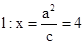 与
与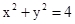 相离,
相离,
过直线上任意一点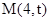 可作圆
可作圆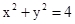 的两条切线
的两条切线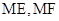 …………10分
…………10分
所以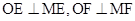
所以O,E,M,F四点都在以OM为直径的圆上, …………………………11分
其方程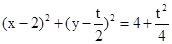 ④ …………………………12分
④ …………………………12分
EF为两圆的公共弦,③-④得:EF的方程为4X+ty -4=0 ………13分
显然无论t为何值,直线ef经过定点(1,0). ………………14分


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,其右准线上
,其右准线上![]() 上存在点
上存在点![]() (点
(点![]() 在
在![]() 轴上方),使
轴上方),使![]() 为等腰三角形.
为等腰三角形.
⑴求离心率![]() 的范围;
的范围;
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三下学期假期检测考试理科数学试卷 题型:解答题
已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
点
,
点 是椭圆的一个顶点,△
是椭圆的一个顶点,△ 是等腰直角三角形.
是等腰直角三角形.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点 分别作直线
分别作直线 ,
, 交椭圆于
交椭圆于 ,
, 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为 ,
, ,且
,且 ,证明:直线
,证明:直线 过定点(
过定点( ).
).
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省三明市高三上学期三校联考数学理卷 题型:解答题
(本题满分14分) 已知椭圆 的左、右焦点分别为F1、F2,其中
的左、右焦点分别为F1、F2,其中
F2也是抛物线 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且
(I)求椭圆C1的方程; (II)已知菱形ABCD的顶点A、C在椭圆C1上,顶点B、D在直线 上,求直线AC的方程。
上,求直线AC的方程。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年云南省德宏州高三高考复习数学试卷 题型:解答题
(本小题满分12分)
已知椭圆 的左、右焦点分别为
的左、右焦点分别为 、
、 ,离心率
,离心率 ,右准线方程为
,右准线方程为 .
.
(I)求椭圆的标准方程;
(II)过点 的直线
的直线 与该椭圆交于M、N两点,且
与该椭圆交于M、N两点,且 ,求直线
,求直线 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com