
(本小题12分)已知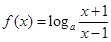 (
(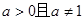 ).
).
(1)判断函数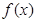 的奇偶性,并证明;
的奇偶性,并证明;
(2)若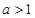 ,用单调性定义证明函数
,用单调性定义证明函数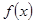 在区间
在区间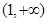 上单调递减;
上单调递减;
(3)是否存在实数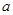 ,使得
,使得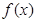 的定义域为
的定义域为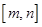 时,值域为
时,值域为
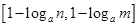 ,若存在,求出实数
,若存在,求出实数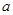 的取值范围;若不存在,则说明理由.
的取值范围;若不存在,则说明理由.
(1)奇函数.(2)函数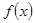 在区间
在区间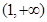 上单调递减.
上单调递减.
(3)满足题目条件的实数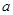 存在,实数
存在,实数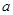 的取值范围是
的取值范围是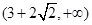 .
.
【解析】
试题分析:(1)根据对数函数的真数大于0建立不等式,解之即可求出函数的定义域,判定是否对称,然后根据函数奇偶性的定义进行判定即可;
(2)任取x1,x2∈(1,+∞),且x1<x2,然后比较真数的大小,从而得到f(x1)与f(x2)的大小,最后根据单调性的定义进行判定即可;
(3)假设存在实数a满足题目条件,然后根据函数在区间[m,n]上单调性建立等式关系,然后转化成方程x2+(1-a)x+a=0在区间(1,+∞)上有两个不同的实根,从而可求出a的取值范围.
解:(1)由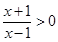 得:
得: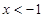 或
或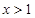 .
.
所以,函数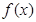 的定义域为
的定义域为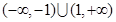 .
.
又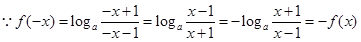
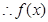 为奇函数.
为奇函数.
(2)任取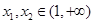 ,且
,且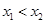 ,则
,则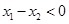 .
.
因为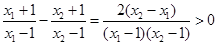
所以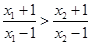 ,又因为
,又因为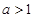 ,所以
,所以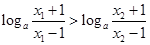 ,
,
故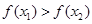 ,所以,函数
,所以,函数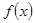 在区间
在区间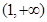 上单调递减.
上单调递减.
(3)假设存在实数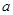 满足题目条件.
满足题目条件.
由题意得: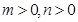 ,又
,又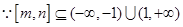 ,
,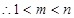
又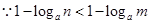 ,
, ,
,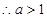 .
.
故,由(2)得:函数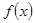 在区间
在区间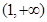 上单减.所以,函数
上单减.所以,函数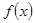 在区间
在区间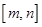 上单调递减.
上单调递减.
故,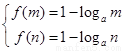 ,所以
,所以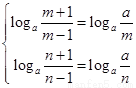 ,
,
所以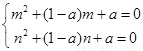 ,
,
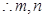 是方程
是方程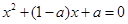 的两个不同的实根.
的两个不同的实根.
故,方程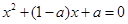 在区间
在区间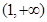 上有两个不同的实根.
上有两个不同的实根.
则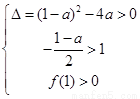 ,解得:
,解得: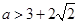 .又
.又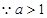 ,
,
所以,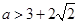 所以,满足题目条件的实数
所以,满足题目条件的实数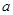 存在,实数
存在,实数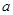 的取值范围是
的取值范围是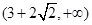 .
.
考点:本题主要考查了函数奇偶性的判定,以及单调性的判定和奇偶性与单调性的综合应用,同时考查了转化的思想,属于中档题.
点评:解决该试题的关键是对于方程在某个区间上方有几个不同的实数根的问题,常常转化为分析参数来求解其范围。


科目:高中数学 来源: 题型:
(本小题12分)已知![]() ,
,![]() ,直线
,直线![]() 与函数
与函数![]() 、
、![]() 的k*s#5^u图象都相切,且与函数
的k*s#5^u图象都相切,且与函数![]() 的k*s#5^u图象的k*s#5^u切点的k*s#5^u横坐标为
的k*s#5^u图象的k*s#5^u切点的k*s#5^u横坐标为![]() .
.
(Ⅰ)求直线![]() 的k*s#5^u方程及
的k*s#5^u方程及![]() 的k*s#5^u值;
的k*s#5^u值;
(Ⅱ)若![]() (其中
(其中![]() 是
是![]() 的k*s#5^u导函数),求函数
的k*s#5^u导函数),求函数![]() 的k*s#5^u最大值;
的k*s#5^u最大值;
(Ⅲ)当![]() 时,求证:
时,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源:2011年四川省泸县二中高2013届春期重点班第一学月考试数学试题 题型:解答题
(本小题12分)已知等比数列 中,
中, 。
。
(1)求数列 的通项公式;
的通项公式;
(2)设等差数列 中,
中, ,求数列
,求数列 的前
的前 项和
项和 .
.
查看答案和解析>>
科目:高中数学 来源:2011云南省潞西市高二上学期期末考试数学试卷 题型:解答题
(本小题12分)
已知顶点在原点,焦点在 轴上的抛物线与直线
轴上的抛物线与直线 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|= ,求抛物线的方程
,求抛物线的方程
查看答案和解析>>
科目:高中数学 来源:2010年浙江省杭州市七校高二上学期期中考试数学文卷 题型:解答题
(本小题12分)
已知圆C: ;
;
(1)若直线 过
过 且与圆C相切,求直线
且与圆C相切,求直线 的方程.
的方程.
(2)是否存在斜率为1直线 ,使直线
,使直线 被圆C截得弦AB,以AB为直径的圆经过原点O. 若存在,求
被圆C截得弦AB,以AB为直径的圆经过原点O. 若存在,求
出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2012届山东省兖州市高二下学期期末考试数学(文) 题型:解答题
(本小题12分)已知函数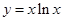
(1) 求这个函数的导数;
(2) 求这个函数的图像在点 处的切线方程。
处的切线方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com