
(09年东城区二模文)(14分)
如图,四棱锥![]() 的底面
的底面![]() 为正方形,
为正方形,![]() 底面
底面![]() ,且
,且![]() ,
,![]() 是
是![]() 中点.
中点.
(Ⅰ)证明:![]() //平面
//平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
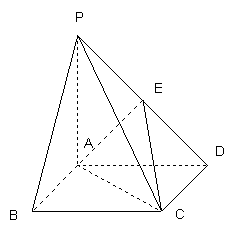
解析: (Ⅰ)
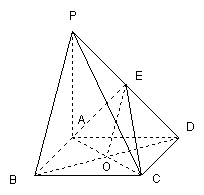
证明:连结![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .
.
![]()
![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点,
中点,
∴![]() //
//![]() . …………………3分
. …………………3分
![]()
![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,
∴ ![]() //平面
//平面![]() . …………………6分
. …………………6分
(Ⅱ)
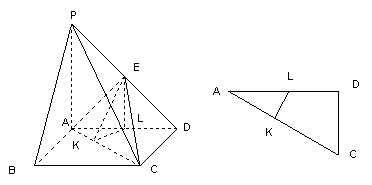
解法1:取![]() 中点
中点![]() ,过
,过![]() 作
作![]()
![]()
![]() 于
于![]() ,连结
,连结![]() 、
、![]() ,
,
![]()
![]() 为
为![]() 中点,∴
中点,∴ ![]() //
//![]() ,∴
,∴ ![]()
![]() 平面
平面![]() ,
,
∴ ![]() 为
为![]() 在平面
在平面![]() 内的射影.
内的射影.
又![]()
![]()
![]() , ∴
, ∴ ![]()
![]()
![]() ,
,
∴![]() 为二面角
为二面角![]() 的平面角. ………………10分
的平面角. ………………10分
在Rt![]()
![]() 中,
中,![]()
![]()
![]() ,
,
∴△![]() ∽△
∽△![]() .
.
∴![]() ,设正方形边长为2,
,设正方形边长为2, ![]() ,∴
,∴ 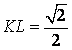 . …………12分
. …………12分
在Rt△![]() 中,
中,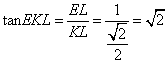 ,
,
∴二面角![]() 的大小为
的大小为![]() . …………14分
. …………14分
解法2:
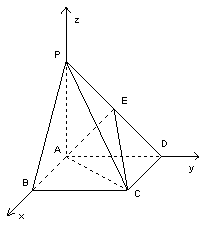
(Ⅱ)如图,以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() . ………………8分
. ………………8分
由![]() ,设正方形边长为2, 则
,设正方形边长为2, 则![]() (0, 0, 0),
(0, 0, 0), ![]() (2, 0, 0),
(2, 0, 0),![]() (2, 2, 0),
(2, 2, 0),
![]() (0, 2, 0),
(0, 2, 0), ![]() (0, 0, 2),
(0, 0, 2), ![]() (0, 1, 1) . ……………10分
(0, 1, 1) . ……………10分
![]()
![]()
![]() 平面
平面![]() ,∴
,∴![]() 是平面
是平面![]() 的法向量,
的法向量, ![]() =(0, 0, 2).
=(0, 0, 2).
设平面![]() 的法向量为
的法向量为![]() ,
, ![]() ,
,
则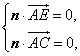 即
即![]() 解得
解得 ![]()
令![]() ,则
,则![]() . …………..12分
. …………..12分
![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
(09年东城区二模文)(14分)
位于函数![]() 的图象上的一系列点
的图象上的一系列点![]() ,这一系列点的横坐标构成以
,这一系列点的横坐标构成以![]() 为首项,
为首项,![]() 为公差的等差数列
为公差的等差数列![]() .
.
(Ⅰ)求点![]() 的坐标;
的坐标;
(Ⅱ)设抛物线![]() 中的每一条的对称轴都垂直于
中的每一条的对称轴都垂直于![]() 轴,对于
轴,对于![]() 第
第![]() 条抛物线
条抛物线![]() 的顶点为
的顶点为![]() ,抛物线
,抛物线![]() 过点
过点![]() ,且在该点处的切线的斜率为
,且在该点处的切线的斜率为![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年东城区二模文)(13分)
在一次抗洪抢险中,准备用射击的方法引爆从河上游漂流而下的一只巨大汽油罐.已知只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功.每次射击命中的概率都是![]() ,每次命中与否互相独立.
,每次命中与否互相独立.
(Ⅰ)求恰用3发子弹就将油罐引爆的概率;
(Ⅱ)求油罐被引爆的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年东城区二模文)(13分)
已知函数![]() 与
与![]() 的图象都过点
的图象都过点![]() (2,0),且在点
(2,0),且在点![]() 处有相同的切线.
处有相同的切线.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)设函数![]() ,求
,求![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com