
【题目】已知函数f(x)= ![]() x2﹣ax+(3﹣a)lnx,a∈R.
x2﹣ax+(3﹣a)lnx,a∈R.
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线2x﹣y+1=0垂直,求a的值;
(2)设f(x)有两个极值点x1 , x2 , 且x1<x2 , 求证:﹣5﹣f(x1)<f(x2)<﹣ ![]() .
.
【答案】
(1)解:∵f′(x)= ![]() ,∴f′(1)=4﹣2a,
,∴f′(1)=4﹣2a,
由题意4﹣2a=﹣ ![]() ,解得:a=
,解得:a= ![]()
(2)解:证明:由题意,x1,x2为f′(x)=0的两根,
∴  ,∴2<a<3,
,∴2<a<3,
由x1+x2=a>2,x1x2=3﹣a<1,知x1<1<x2,
结合单调性有f(x2)<f(1)= ![]() ﹣a<﹣
﹣a<﹣ ![]() ,
,
又f(x1)+f(x2)= ![]() (
( ![]() +
+ ![]() )﹣a(x1+x2)+(3﹣a)lnx1x2=﹣
)﹣a(x1+x2)+(3﹣a)lnx1x2=﹣ ![]() a2+a﹣3+(3﹣a)ln(3﹣a),
a2+a﹣3+(3﹣a)ln(3﹣a),
设h(a)=﹣ ![]() a2+a﹣3+(3﹣a)ln(3﹣a),a∈(2,3),
a2+a﹣3+(3﹣a)ln(3﹣a),a∈(2,3),
则h′(a)=﹣a﹣ln(3﹣a),
h″(a)= ![]() >0,故h′(a)在(2,3)递增,又h′(2)=﹣2<0,
>0,故h′(a)在(2,3)递增,又h′(2)=﹣2<0,
a→3时,h′(a)→+∞,
∴a0∈(2,3),当a∈(2,a0)时,h(a)递减,当a∈(a0,3)时,h(a)递增,
∴h(a)min=h(a0)=﹣ ![]()
![]() +a0﹣3+(3﹣a0)(﹣a0)=
+a0﹣3+(3﹣a0)(﹣a0)= ![]()
![]() ﹣2a0﹣3>﹣5,
﹣2a0﹣3>﹣5,
∴a∈(2,3),h(a)>﹣5,
综上,﹣5﹣f(x1)<f(x2)<﹣ ![]()
【解析】(1)求出函数的导数,根据f′(1)的值,求出a的值;(2)根据x1 , x2是方程f′(x)=0的根,得到关于a的不等式组,求出a的范围,求出f(x1)+f(x2)的表达式,设h(a)=﹣ ![]() a2+a﹣3+(3﹣a)ln(3﹣a),a∈(2,3),根据函数的单调性证明即可.
a2+a﹣3+(3﹣a)ln(3﹣a),a∈(2,3),根据函数的单调性证明即可.
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2﹣4ax+3a2<0,其中a>0; q:实数x满足 ![]() <0.
<0.
(1)若a=1,且p∨q为真,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 作曲线
作曲线![]() (其中
(其中![]() 为自然对数的底数)的切线,切点为
为自然对数的底数)的切线,切点为![]() ,设
,设![]() 在
在![]() 轴上的投影是点
轴上的投影是点![]() ,过点
,过点![]() 再作曲线
再作曲线![]() 的切线,切点为
的切线,切点为![]() ,设
,设![]() 在
在![]() 轴上的投影是点
轴上的投影是点![]() ,依次下去,得到第
,依次下去,得到第![]() 个切点
个切点![]() ,则点
,则点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左右顶点为
的左右顶点为![]() ,右焦点为
,右焦点为![]() ,一条准线方程是
,一条准线方程是![]() ,点
,点![]() 为椭圆
为椭圆![]() 上异于
上异于![]() 的两点,点
的两点,点![]() 为
为![]() 的中点.
的中点.
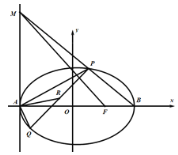
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交直线
交直线![]() 于点
于点![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)若![]() ,求直线
,求直线![]() 斜率的取值范围。
斜率的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x+2|﹣|x﹣2|. (Ⅰ)求不等式f(x)>2的解集;
(Ⅱ)若x∈R,f(x)≥t2﹣ ![]() t恒成立,求实数t的取值范围.
t恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有人持金出五关,前关二而税一,次关三而税一,次关四而税一,次关五而税一,次关六而税一,并五关所税,适重一斤,问本持金几何”其意思为“今有人持金出五关,第1关收税金 ![]() ,第2关收税金为剩余金的
,第2关收税金为剩余金的 ![]() ,第3关收税金为剩余金的
,第3关收税金为剩余金的 ![]() ,第4关收税金为剩余金的
,第4关收税金为剩余金的 ![]() ,第5关收税金为剩余金的
,第5关收税金为剩余金的 ![]() ,5关所收税金之和,恰好重1斤,问原来持金多少?”若将题中“5关所收税金之和,恰好重1斤,问原来持金多少?”改成假设这个原来持金为x,按此规律通过第8关,则第8关需收税金为x.
,5关所收税金之和,恰好重1斤,问原来持金多少?”若将题中“5关所收税金之和,恰好重1斤,问原来持金多少?”改成假设这个原来持金为x,按此规律通过第8关,则第8关需收税金为x.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆:![]() 的四个顶点围成的四边形的面积为
的四个顶点围成的四边形的面积为![]() ,原点到直线
,原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知定点![]() ,是否存在过
,是否存在过![]() 的直线
的直线![]() ,使
,使![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 的左顶点?若存在,求出
的左顶点?若存在,求出![]() 的方程:若不存在,请说明理由.
的方程:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinωx﹣ ![]() cosωx(ω>0),若方程f(x)=﹣1在(0,π)上有且只有四个实数根,则实数ω的取值范围为( )
cosωx(ω>0),若方程f(x)=﹣1在(0,π)上有且只有四个实数根,则实数ω的取值范围为( )
A.( ![]() ,
, ![]() ]
]
B.( ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() ]
]
D.( ![]() ,
, ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com