练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本大题12分）

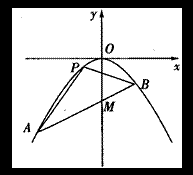    如图，抛物线的项点O在坐标原点，焦点在y轴负半轴上，过点M（0，-2）作直线与抛物线相交于A，B两点，且满足（I）求直线和抛物线的方程；

       （II）当抛物线上一动点P从点A向点B运动时，求面积的最大值。

    (Ⅰ) 直线的方程为，抛物线的方程为   (Ⅱ)   


    解析:

    （I）据题意可设直线的方程为

    抛物线的方程为 （2分）

    由（3分），设点则

    所以   （4分）

    因为所以（5分）

        故直线的方程为，抛物线的方程为  （6分）

       （II）解法一：据题意，当抛物线过点P的切线与平行时，的面积最大。（7分）

        设点    因为

        所以P（-2，-2）。     （9分）此时，点P到直线的距离

    （10分） 由

        所以

    故的面积的最大值为   （12分）

    解法二：由（7分）

        所以（8分）

        设点，点P到直线的距离为d。 （9分）

        则

        当

       故的面积的最大值为    （12分）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （本大题12分）

    如图，直四棱柱中，，，，,与交于点．

       （Ⅰ）求证：；

       （Ⅱ）求二面角的大小；

       （Ⅲ）求异面直线与所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年浙江杭州高二12月月考理科数学试卷（解析版） 题型：解答题

    （本大题12分）如图，在棱长为ɑ的正方体ABCD-A1B1C1D1中，E、F、G分别是CB、CD、CC1的中点．

    （1）求直线C与平面ABCD所成角的正弦的值；

    （2）求证：平面A B1D1∥平面EFG；

    （3）求证：平面AA1C⊥面EFG ．

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年江西省高三第一次月考理科数学试卷 题型：解答题

    （本小题12分）如图，函数y=|x|在x∈[－1,1]的图象上有两点A、B，AB∥

     

    Ox轴，点M（1，m）（m是已知实数，且m>）是△ABC的边BC的中点。

     

    （Ⅰ）写出用B的横坐标t表示△ABC面积S的函数解析式S＝f(t)；

    （Ⅱ）求函数S＝f(t)的最大值，并求出相应的C点坐标。

     

     

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011年福建省高二下学期期中考试理数 题型：解答题

    （本小题12分）

    如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN，要求M在AB的延长线上，N在AD的延长线上，且对角线MN过C点。已知AB=3米，AD=2米。设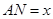（单位：米），若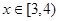（单位：米），则当AM，AN的长度分别是多少时，花坛AMPN的面积最大？并求出最大面积。

     

     

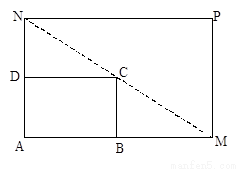
    查看答案和解析>>

    同步练习册答案