解 (1)∵椭圆方程为
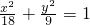
∴a
2=18,b
2=9,得c=

=3,可得F(3,0)…(1分)

∵
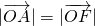
且点A在x轴的上方,…(2分)
∴可得A在椭圆上且
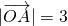
,得A是椭圆的上顶点,坐标为A(0,3)
由此可得l的斜率k=-1,
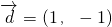
…(3分)
因此,直线l的方程为:

,化简得x+y-3=0…(4分)
(2)设A(x
1,y
1)、B(x
2,y
2),直线l:y=k(x-3)…(5分)
将直线与椭圆方程联列
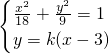
,…(6分)
消去x,得(1+2k
2)y
2+6ky-9k
2=0…(7分)
由于△>0恒成立,根据根与系数的关系可得
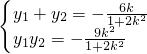
…(8分)
∴

…(9分)
因此,可得S
△PAB=
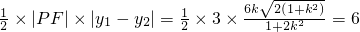
化简整理,得k
4-k
2-2=0,由于k>0,解之得k=1…(10分)
(3)假设存在这样的点C(x
0,0),使得直线AC和BC的斜率之和为0,
根据题意,得直线l:y=k(x-3)(k≠0)
由
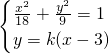
消去y,得(1+2k
2)x
2-12k
2x+18(k
2-1)=0…(12分)
由于△>0恒成立,根据根与系数的关系可得
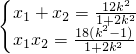
…(*)…(13分)
而

,

,…(14分)
∴
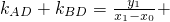

=

由此化简,得2kx
1x
2-k(x
0+3)(x
1+x
2)+6kx
0=0,…(15分)
将(*)式代入,可得
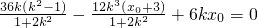
,解之得x
0=6,
∴存在一点C(6,0),使得直线AC和BC的斜率之和为0.…(16分)
分析:(1)根据椭圆方程,算出右焦点F坐标为(3,0),结合椭圆上位于x轴上方的点A满足
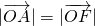
算出A(0,3),由此可得直线l的斜率k=-1,即可求出直线l的方程;
(2)设直线l:y=k(x-3),与椭圆方程联解消去y得(1+2k
2)y
2+6ky-9k
2=0,由根与系数的关系算出AB的纵坐标之差的绝对值关于k的式子,再根据△PAB的面积为6建立关于k的方程,化简整理得k
4-k
2-2=0,解之得k=1(舍负);
(3)设直线l方程为y=k(x-3)与椭圆方程联解消去y得(1+2k
2)x
2-12k
2x+18(k
2-1)=0,由根与系数的关系得到
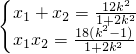
,然后化简k
AD+k
BD=0为关于x
1、y
1、x
2、y
2和x
0的等式,化简整理得2kx
1x
2-k(x
0+3)(x
1+x
2)+6kx
0=0,再将前面算出的x
1+x
2和x
1x
2的表达式代入化简可得x
0=6,由此可得存在一点C(6,0),使得直线AC和BC的斜率之和为0.
点评:本题给出椭圆方程,在直线l经过椭圆的右焦点F且交椭圆于A、B两点且满足
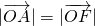
的情况下求直线l的方程,并且讨论了x轴上是否存在一点C使得直线AC和BC的斜率之和为0的问题.着重考查了椭圆的标准方程与简单几何性质、一元二次方程根与系数的关系和直线与圆锥曲线的位置关系等知识点,属于中档题.

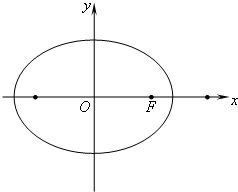
 在平面直角坐标系xOy中,方向向量为
在平面直角坐标系xOy中,方向向量为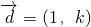 的直线l经过椭圆
的直线l经过椭圆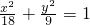 的右焦点F,与椭圆相交于A、B两点
的右焦点F,与椭圆相交于A、B两点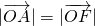 ,求直线l的方程;
,求直线l的方程;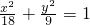
 =3,可得F(3,0)…(1分)
=3,可得F(3,0)…(1分)
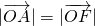 且点A在x轴的上方,…(2分)
且点A在x轴的上方,…(2分)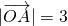 ,得A是椭圆的上顶点,坐标为A(0,3)
,得A是椭圆的上顶点,坐标为A(0,3)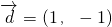 …(3分)
…(3分) ,化简得x+y-3=0…(4分)
,化简得x+y-3=0…(4分)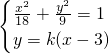 ,…(6分)
,…(6分)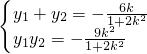 …(8分)
…(8分) …(9分)
…(9分)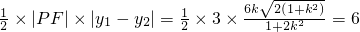
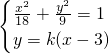 消去y,得(1+2k2)x2-12k2x+18(k2-1)=0…(12分)
消去y,得(1+2k2)x2-12k2x+18(k2-1)=0…(12分)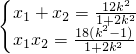 …(*)…(13分)
…(*)…(13分)  ,
, ,…(14分)
,…(14分)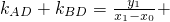


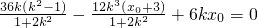 ,解之得x0=6,
,解之得x0=6,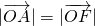 算出A(0,3),由此可得直线l的斜率k=-1,即可求出直线l的方程;
算出A(0,3),由此可得直线l的斜率k=-1,即可求出直线l的方程;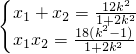 ,然后化简kAD+kBD=0为关于x1、y1、x2、y2和x0的等式,化简整理得2kx1x2-k(x0+3)(x1+x2)+6kx0=0,再将前面算出的x1+x2和x1x2的表达式代入化简可得x0=6,由此可得存在一点C(6,0),使得直线AC和BC的斜率之和为0.
,然后化简kAD+kBD=0为关于x1、y1、x2、y2和x0的等式,化简整理得2kx1x2-k(x0+3)(x1+x2)+6kx0=0,再将前面算出的x1+x2和x1x2的表达式代入化简可得x0=6,由此可得存在一点C(6,0),使得直线AC和BC的斜率之和为0.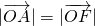 的情况下求直线l的方程,并且讨论了x轴上是否存在一点C使得直线AC和BC的斜率之和为0的问题.着重考查了椭圆的标准方程与简单几何性质、一元二次方程根与系数的关系和直线与圆锥曲线的位置关系等知识点,属于中档题.
的情况下求直线l的方程,并且讨论了x轴上是否存在一点C使得直线AC和BC的斜率之和为0的问题.着重考查了椭圆的标准方程与简单几何性质、一元二次方程根与系数的关系和直线与圆锥曲线的位置关系等知识点,属于中档题. 

 (2013•普陀区二模)在平面直角坐标系xOy中,方向向量为
(2013•普陀区二模)在平面直角坐标系xOy中,方向向量为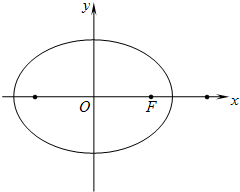 (2013•普陀区二模)在平面直角坐标系xOy中,方向向量为
(2013•普陀区二模)在平面直角坐标系xOy中,方向向量为 的直线l经过椭圆
的直线l经过椭圆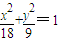 的右焦点F,与椭圆相交于A、B两点
的右焦点F,与椭圆相交于A、B两点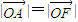 ,求直线l的方程;
,求直线l的方程;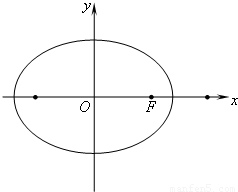
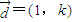 的直线l经过椭圆
的直线l经过椭圆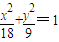 的右焦点F,与椭圆相交于A、B两点
的右焦点F,与椭圆相交于A、B两点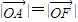 ,求直线l的方程;
,求直线l的方程;