
 BC,
BC,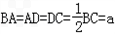 ,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使面B1AE⊥面AECD,F为B1D的中点.
,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使面B1AE⊥面AECD,F为B1D的中点. 面ACF;
面ACF;
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| AB |
| BC |
| CB |
| CD |
| CD |
| DA |
| DA |
| AB |
| A、平行四边形 | B、梯形 |
| C、平面四边形 | D、空间四边形 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•铁岭模拟)已知四边形ABCD满足AD∥BC,BA=AD=DC=
(2013•铁岭模拟)已知四边形ABCD满足AD∥BC,BA=AD=DC=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| AB |
| BC |
| CB |
| CD |
| CD |
| DA |
| DA |
| AB |
| A.平行四边形 | B.梯形 | C.平面四边形 | D.空间四边形 |
查看答案和解析>>
科目:高中数学 来源:《3.2 立体几何中的向量方法》2011年同步练习1(人教A版-选修2-1)(解析版) 题型:选择题
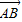 •
• >0,
>0,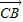 •
•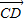 >0,
>0,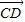 •
•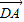 >0,
>0,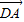 •
•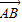 >0,则该四边形为( )
>0,则该四边形为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com